题目内容
9.已知方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,那么方程组$\left\{\begin{array}{l}{{a}_{1}(x-1)+{b}_{1}(y+2)={c}_{1}}\\{{a}_{2}(x-1)+{b}_{2}(y+2)={c}_{2}}\end{array}\right.$的解为( )| A. | $\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=-5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=-5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ |
分析 根据对应相等,由方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,可以得到方程组$\left\{\begin{array}{l}{{a}_{1}(x-1)+{b}_{1}(y+2)={c}_{1}}\\{{a}_{2}(x-1)+{b}_{2}(y+2)={c}_{2}}\end{array}\right.$的解,本题得以解决.
解答 解:∵方程组$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,
∴在方程组$\left\{\begin{array}{l}{{a}_{1}(x-1)+{b}_{1}(y+2)={c}_{1}}\\{{a}_{2}(x-1)+{b}_{2}(y+2)={c}_{2}}\end{array}\right.$中,$\left\{\begin{array}{l}{x-1=2}\\{y+2=-3}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=3}\\{y=-5}\end{array}\right.$,
故选B.
点评 本题考查二元一次方程组的解,解答本题的关键是明确解二元一次方程组的方法,找准对应关系.

| A. | a${\;}^{\frac{1}{2}}$ | B. | a-1 | C. | a-2 | D. | a13 |
 如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )
如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在B处,两边与CD及其延长线交于E,F,若CE=1,则BF的长为( )| A. | 2$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | $\frac{8}{3}$$\sqrt{10}$ |
 如图,AB∥CD∥EF,则下列各式中正确的是( )
如图,AB∥CD∥EF,则下列各式中正确的是( )| A. | ∠1=180°-∠3 | B. | ∠1=∠3-∠2 | C. | ∠2+∠3=180°-∠1 | D. | ∠2+∠3=180°+∠1 |
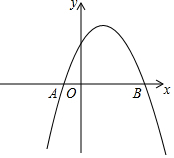 如图,已知抛物线y=-x2+bx+c经过A(-1,0),B(3,0)两点.
如图,已知抛物线y=-x2+bx+c经过A(-1,0),B(3,0)两点. .
.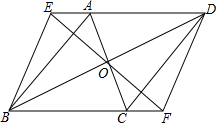 已知:如图,?ABCD中,对角线AC、BD交于点O,直线EF经过点O,分别交DA,BC的延长线于点E,F,连接BE,DF.
已知:如图,?ABCD中,对角线AC、BD交于点O,直线EF经过点O,分别交DA,BC的延长线于点E,F,连接BE,DF.