题目内容
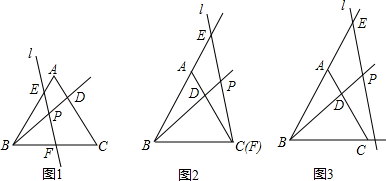
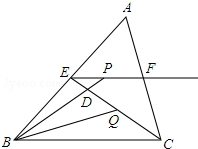如图所示，在△ABC中，E、F分别是AB、AC的中点，BC=6，CE=5，动点P在射线EF上，BP交CE于D，∠CBP的平分线交CE于Q，当EP+BP=18时，则CQ的值为考点：相似三角形的判定与性质
专题：
分析：如图，作辅助线；证明∠PBM=∠PMB，得到PM=PB，此为解题的关键性结论；证明△EMQ∽△CBQ得到
=
，根据BC=6，CQ+EQ=5，求出CQ．
| EM |
| BC |
| EQ |
| CQ |
解答：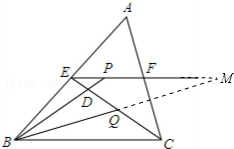
解：如图，延长BQ，交EF的延长线于点M；
∵∠CBP的平分线交CE于Q，
∴∠PBM=∠CBM；
∵E、F分别是AB、AC的中点，
∴EF∥BC，∠PMB=∠CBM，
∴∠PBM=∠PMB，PM=PB，
∴EM=PE+PM=PE+PB=18；
∵EF∥BC，
∴△EMQ∽△CBQ，
∴
=
，而BC=6，CQ+EQ=5，
∴CQ=
，故答案为
．
解：如图，延长BQ，交EF的延长线于点M；∵∠CBP的平分线交CE于Q，
∴∠PBM=∠CBM；
∵E、F分别是AB、AC的中点，
∴EF∥BC，∠PMB=∠CBM，
∴∠PBM=∠PMB，PM=PB，
∴EM=PE+PM=PE+PB=18；
∵EF∥BC，
∴△EMQ∽△CBQ，
∴
| EM |
| BC |
| EQ |
| CQ |
∴CQ=
| 5 |
| 4 |
| 5 |
| 4 |
点评：该题主要考查了相似三角形的判定及其性质、等腰三角形的判定等几何知识点及其应用问题；解题的关键是作辅助线，构造相似三角形．
练习册系列答案
名校课堂系列答案
相关题目
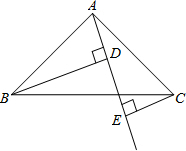如图，已知△ABC中，∠BAC=90°，AB=AC，AE是过点A的一条直线，且B点和C点在AE的两侧，BD⊥AE于点D，CE⊥AE于点E．
如图，将甲图经过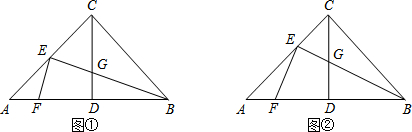
如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=4cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜12），连接DE，当△BDE是直角三角形时，t的值为
DE为△ABC的中位线，连接BE，且BE=BC，延长DE到点F，使EF=BE，连接CF，BF．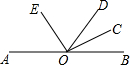
如图，AB是一条直线，OD是一条射线，OV，OE分别是∠BOD，∠AOD的平分线，∠BOC=15°48′．