题目内容
已知:点D是等边三角形ABC边AC上一点,点P是射线BD上的一动点,过点P的直线l与AB,BC所在直线分别相交于点E,F,且∠BPF=60°
(1)如图1,写出图中所有与△BPF相似的三角形;
(2)若等边三角形ABC的边长为3,将直线l向右平移,当点F与点C重合时(如图2)所示,求BD•BP的值.
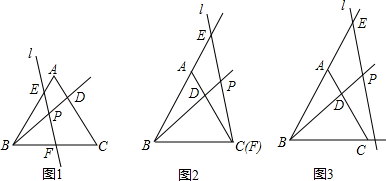
(1)如图1,写出图中所有与△BPF相似的三角形;
(2)若等边三角形ABC的边长为3,将直线l向右平移,当点F与点C重合时(如图2)所示,求BD•BP的值.

考点:相似三角形的判定与性质
专题:
分析:(1)由∠C=∠BPF,∠DBC=∠FBP,易证△BCD∽△BPF;
(2)先证明△BCD∽△BPC,得出比例式
=
,因此BD•BP=BC2=32=9.
(2)先证明△BCD∽△BPC,得出比例式
| BC |
| BP |
| BD |
| BC |
解答:解:(1)△BCD∽△BPF;
∵△ABC是等边三角形,
∴∠C=60°,
∵∠BPF=60°,
∴∠C=∠BPF,
又∵∠DBC=∠FBP,
∴△BCD∽△BPF;
(2)∵△ABC是等边三角形,
∴∠C=60°,BC=3,
∵∠BPC=60°,
∴∠C=∠BPC,
又∵∠DBC=∠CBP,
∴△BCD∽△BPC,
∴
=
,
∴BD•BP=BC2=32=9.
∵△ABC是等边三角形,
∴∠C=60°,
∵∠BPF=60°,
∴∠C=∠BPF,
又∵∠DBC=∠FBP,
∴△BCD∽△BPF;
(2)∵△ABC是等边三角形,
∴∠C=60°,BC=3,
∵∠BPC=60°,
∴∠C=∠BPC,
又∵∠DBC=∠CBP,
∴△BCD∽△BPC,
∴
| BC |
| BP |
| BD |
| BC |
∴BD•BP=BC2=32=9.
点评:本题考查了相似三角形的判定与性质;证明三角形相似得出比例式是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目

 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E. 如图,在半径为2,圆心角为90°的扇形ACB内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为
如图,在半径为2,圆心角为90°的扇形ACB内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为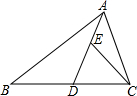 如图所示,AD为△ABC的中线,E为AD上一点,若∠DAC=∠B,CD=CE,求证:
如图所示,AD为△ABC的中线,E为AD上一点,若∠DAC=∠B,CD=CE,求证: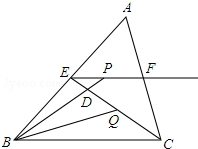 如图所示,在△ABC中,E、F分别是AB、AC的中点,BC=6,CE=5,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当EP+BP=18时,则CQ的值为
如图所示,在△ABC中,E、F分别是AB、AC的中点,BC=6,CE=5,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当EP+BP=18时,则CQ的值为 如图所示的转盘,分成三个相同的扇形,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,视为无效,重新转动一次转盘),此过程称为一次操作.请用树状图或列表法,求事件“两次操作,第一次操作得到的数与第二次操作得到的数的绝对值相等”发生的概率.
如图所示的转盘,分成三个相同的扇形,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,视为无效,重新转动一次转盘),此过程称为一次操作.请用树状图或列表法,求事件“两次操作,第一次操作得到的数与第二次操作得到的数的绝对值相等”发生的概率.