题目内容
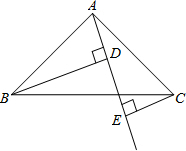 如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.
如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.(1)求证:△ABD≌△CAE;
(2)若BD=2.5,DE=1.7,求CE的长.
考点:全等三角形的判定与性质
专题:
分析:(1)利用直角三角形的两锐角互余以及余角的性质即可证得∠ABD=∠CAE,则利用AAS即可证得△ABD≌△CAE;
(2)根据△ABD≌△CAE可以证得AE=BD,AD=CE,然后根据CE=AD=AE-DE即可求解.
(2)根据△ABD≌△CAE可以证得AE=BD,AD=CE,然后根据CE=AD=AE-DE即可求解.
解答:解:(1)证明:∵∠BAE+∠CAE=90°,
又∵直角△ABD中,∠BAE+∠ABD=90°,
∴∠ABD=∠CAE.
则在△ABD和△ACE中,
,
∴△ABD≌△CAE;
(2)∵△ABD≌△CAE,
∴AE=BD,AD=CE,
∴CE=AD=AE-DE=2.5-1.7=0.8.
又∵直角△ABD中,∠BAE+∠ABD=90°,
∴∠ABD=∠CAE.
则在△ABD和△ACE中,
|
∴△ABD≌△CAE;
(2)∵△ABD≌△CAE,
∴AE=BD,AD=CE,
∴CE=AD=AE-DE=2.5-1.7=0.8.
点评:本题考查了全等三角形的判定与性质,正确根据直角三角形的两内角互余以及余角的性质证明∠ABD=∠CAE是关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 如图所示,在直角三角形外边有三个正方形,其中有两个面积为S1=169,S2=144,则S3为( )
如图所示,在直角三角形外边有三个正方形,其中有两个面积为S1=169,S2=144,则S3为( )| A、25 | B、30 | C、50 | D、100 |
 .
.

 如图,AC、BC是⊙O的两条弦,其中BC>AC,半径OD⊥AB,DE⊥BC于E,
如图,AC、BC是⊙O的两条弦,其中BC>AC,半径OD⊥AB,DE⊥BC于E, 如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.
如图,△ABC的边AB为⊙O的直径,BC与圆交于点D,D为BC的中点,过D作DE⊥AC于E.



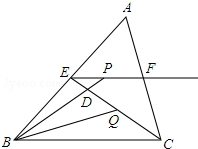 如图所示,在△ABC中,E、F分别是AB、AC的中点,BC=6,CE=5,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当EP+BP=18时,则CQ的值为
如图所示,在△ABC中,E、F分别是AB、AC的中点,BC=6,CE=5,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当EP+BP=18时,则CQ的值为