题目内容
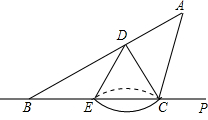 如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥体底面圆的圆心,圆锥体的离为2
如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥体底面圆的圆心,圆锥体的离为2| 3 |
(1)求∠B的度数;
(2)若∠ACP=60°,求光源A距水平面BP的距离.
考点:解直角三角形的应用,勾股定理的应用,圆锥的计算,平行投影
专题:
分析:(1)如下图所示,过点D作DF垂直BC于点F.由题意,得DF=2
,EF=2,BE=4,在Rt△DFB中,tan∠B的值,由此可以求出∠B;
(2)过点A作AH垂直BP于点H.因为∠ACP=2∠B=60°所以∠BAC=30°,AC=BC=8.在Rt△ACH中,AH=AC•Sin∠ACP,所以可以求出AH了,即求出了光源A距平面的高度.
| 3 |
(2)过点A作AH垂直BP于点H.因为∠ACP=2∠B=60°所以∠BAC=30°,AC=BC=8.在Rt△ACH中,AH=AC•Sin∠ACP,所以可以求出AH了,即求出了光源A距平面的高度.
解答:解:(1)过D作DF⊥BC交BC于点F,则DF=2
,EF=2,
∴BF=6.
在Rt△BFD中,由勾股定理,得BD2=BF2+DF2=62+(2
)2=48,
∴BD=4
,
又sin∠B=
=
=
,
∴∠B=30°;
(2)∵∠ACP=60°,
∴∠BAC=30°,
∴AC=BC=8,
过点A作BP的垂线交BP于点M,
在Rt△ACM中,AM=ACsin∠ACM=8sin60°=4
(米),
即光源A距水平面BP的距离为4
米.
| 3 |
∴BF=6.
在Rt△BFD中,由勾股定理,得BD2=BF2+DF2=62+(2
| 3 |

∴BD=4
| 3 |
又sin∠B=
| DF |
| BD |
2
| ||
4
|
| 1 |
| 2 |
∴∠B=30°;
(2)∵∠ACP=60°,
∴∠BAC=30°,
∴AC=BC=8,
过点A作BP的垂线交BP于点M,
在Rt△ACM中,AM=ACsin∠ACM=8sin60°=4
| 3 |
即光源A距水平面BP的距离为4
| 3 |
点评:本题考查了学生运用三角函数知识解决实际问题的能力,又让学生感受到生活处处有数学,数学在生产生活中有着广泛的作用.

练习册系列答案
相关题目
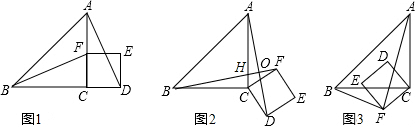
 如图,三个等边三角形如图放置,若∠1=70°,则∠2+∠3=( )
如图,三个等边三角形如图放置,若∠1=70°,则∠2+∠3=( )| A、110° | B、105° |
| C、100° | D、95° |
 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,记四边形A1ABB1的面积为S1;再分别取A1C、B1C的中点A2、B2,记四边形A2A1B1B2的面积为S2;再分别取A2C、B2C的中点A3、B3,依次取下去…
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,记四边形A1ABB1的面积为S1;再分别取A1C、B1C的中点A2、B2,记四边形A2A1B1B2的面积为S2;再分别取A2C、B2C的中点A3、B3,依次取下去…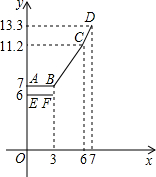 为缓解油价上涨给出租车行业带来的成本压力,某市自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
为缓解油价上涨给出租车行业带来的成本压力,某市自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
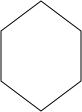 如图,表示一个正六菱柱形状的高大建筑物的俯视图.若该建筑物的高度为150米,底面正六边形的边长为50米.
如图,表示一个正六菱柱形状的高大建筑物的俯视图.若该建筑物的高度为150米,底面正六边形的边长为50米.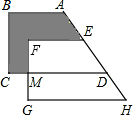 如图所示,把一梯形ABCD沿AD方向平移到角梯形EFGH,梯形ABCD的腰BC分别垂直于两底AB和CD,已知HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是
如图所示,把一梯形ABCD沿AD方向平移到角梯形EFGH,梯形ABCD的腰BC分别垂直于两底AB和CD,已知HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是