题目内容
 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,记四边形A1ABB1的面积为S1;再分别取A1C、B1C的中点A2、B2,记四边形A2A1B1B2的面积为S2;再分别取A2C、B2C的中点A3、B3,依次取下去…
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,记四边形A1ABB1的面积为S1;再分别取A1C、B1C的中点A2、B2,记四边形A2A1B1B2的面积为S2;再分别取A2C、B2C的中点A3、B3,依次取下去…(1)由已知,可求得S1=
(2)利用这一图形,计算
| 3 |
| 4100 |
| 3 |
| 4101 |
| 3 |
| 4102 |
| 3 |
| 4200 |
考点:相似三角形的判定与性质,三角形中位线定理
专题:规律型
分析:(1)首先计算出第一个和第二个、第三个三角形的面积找到规律即可求出问题的答案;
(2)根据(1)中的规律计算即可.
(2)根据(1)中的规律计算即可.
解答:解:(1)∵A1、B1分别是AC、BC两边的中点,
且△ABC的面积为1,
∴△A1B1C的面积为1×
=
.
∴四边形A1ABB1的面积=△ABC的面积-△A1B1C的面积=
=1-
;
∴四边形A2A1B1B2的面积=△A1B1C的面积-△A2B2C的面积=
-
=
.
…,
∴第n个四边形的面积=
,
∴S100=
.
故答案为:
,
,
;
(2)由(1)可知:
+
+
+…+
=(
-
+
-
…-
)=
-
.
且△ABC的面积为1,
∴△A1B1C的面积为1×
| 1 |
| 4 |
| 1 |
| 4 |
∴四边形A1ABB1的面积=△ABC的面积-△A1B1C的面积=
| 3 |
| 4 |
| 1 |
| 4 |
∴四边形A2A1B1B2的面积=△A1B1C的面积-△A2B2C的面积=
| 1 |
| 4 |
| 1 |
| 42 |
| 3 |
| 42 |
…,
∴第n个四边形的面积=
| 3 |
| 4n |
∴S100=
| 3 |
| 4100 |
故答案为:
| 3 |
| 4 |
| 3 |
| 42 |
| 3 |
| 4100 |
(2)由(1)可知:
| 3 |
| 4100 |
| 3 |
| 4101 |
| 3 |
| 4102 |
| 3 |
| 4200 |
| 1 |
| 499 |
| 1 |
| 4100 |
| 1 |
| 4100 |
| 1 |
| 4101 |
| 1 |
| 4200 |
| 1 |
| 499 |
| 1 |
| 4200 |
点评:本题考查了三角形的中位线性质定理和相似三角形的性质,同时也考查了学生通过特例分析从而归纳总结出一般结论的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在已知实数:-1,0,
,-2中,最小的一个实数是( )
| 1 |
| 2 |
| A、-1 | ||
| B、0 | ||
C、
| ||
| D、-2 |
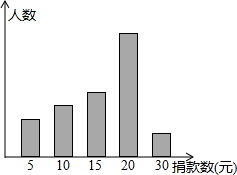 某中学对“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元得人数共39人.
某中学对“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元得人数共39人.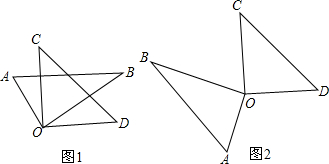 如图,将一副三角板的两个直角顶点O重合在一起,摆放成如图1、图2所示的形状.
如图,将一副三角板的两个直角顶点O重合在一起,摆放成如图1、图2所示的形状.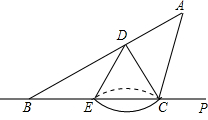 如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥体底面圆的圆心,圆锥体的离为2
如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥体底面圆的圆心,圆锥体的离为2