题目内容
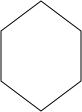 如图,表示一个正六菱柱形状的高大建筑物的俯视图.若该建筑物的高度为150米,底面正六边形的边长为50米.
如图,表示一个正六菱柱形状的高大建筑物的俯视图.若该建筑物的高度为150米,底面正六边形的边长为50米.(1)画出它的主视图;
(2)求该建筑物的体积.
考点:作图-三视图
专题:
分析:(1)根据三视图定义作出主视图即可;
(2)首先求出正六边形面积,进而得出其体积即可.
(2)首先求出正六边形面积,进而得出其体积即可.
解答: 解:(1)如图所示:
解:(1)如图所示:
(2)连接正六变形的中心O和两个顶点D、E,
得到△ODE,
∵∠DOE=360°×
=60°,
又∵OD=OE,
∴∠ODE=∠OED=(180°-60°)÷2=60°,
则三角形ODE为正三角形,
 ∴OD=OE=DE=50,
∴OD=OE=DE=50,
∴S△ODE=
OD•OE•sin60°=
×50×50×
=625
(m2).
正六边形的面积为6×625
=3750
(m2),
故该建筑物的体积为:150×3750
=562500
(m3).
 解:(1)如图所示:
解:(1)如图所示:(2)连接正六变形的中心O和两个顶点D、E,
得到△ODE,
∵∠DOE=360°×
| 1 |
| 6 |
又∵OD=OE,
∴∠ODE=∠OED=(180°-60°)÷2=60°,
则三角形ODE为正三角形,
 ∴OD=OE=DE=50,
∴OD=OE=DE=50,∴S△ODE=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
正六边形的面积为6×625
| 3 |
| 3 |
故该建筑物的体积为:150×3750
| 3 |
| 3 |
点评:此题主要考查了三视图的画法以及正六边形面积求法和立方体体积求法,得出正六边形面积是解题关键.

练习册系列答案
相关题目
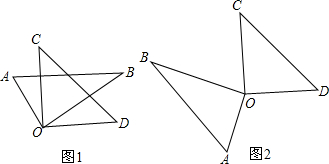 如图,将一副三角板的两个直角顶点O重合在一起,摆放成如图1、图2所示的形状.
如图,将一副三角板的两个直角顶点O重合在一起,摆放成如图1、图2所示的形状.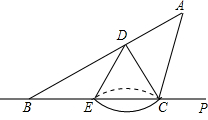 如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥体底面圆的圆心,圆锥体的离为2
如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥体底面圆的圆心,圆锥体的离为2
