题目内容
12.(1)计算:(-1)2014+(sin30°)-1+($\frac{3}{5-\sqrt{2}}$)0-|3-$\sqrt{18}$|+83×(-0.125)3(2)先化简,再求值:$\frac{{x}^{2}+2x+1}{2x-6}$÷(x-$\frac{1-3x}{x-3}$),其中x为数据0,-1,-3,1,2的极差.
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再选取合适的x的值代入进行计算即可.
解答 解:(1)原式=1+2+1-3$\sqrt{2}$+3-(8×0.125)3
=7-3$\sqrt{2}$-1
=6-3$\sqrt{2}$;
(2)原式=$\frac{(x+1)^{2}}{2(x-3)}$÷$\frac{{x}^{2}-3x-x+3{x}^{2}}{x(x-3)}$
=$\frac{{(x+1)}^{2}}{2(x-3)}$÷$\frac{4x(x-1)}{x(x-3)}$
=$\frac{{(x+1)}^{2}}{2(x-3)}$•$\frac{x-3}{4(x-1)}$
=$\frac{(x+1)^{2}}{8(x-1)}$,
∵数据0,-1,-3,1,2的极差=2+3=5,
∴当x=5时,原式=$\frac{{(5+1)}^{2}}{8(5-1)}$=$\frac{36}{32}$=$\frac{9}{8}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
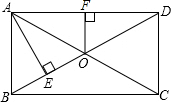 如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BO于E,OF⊥AD于F,已知OF=3cm,且BE:ED=1:3,求BD的长.
如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BO于E,OF⊥AD于F,已知OF=3cm,且BE:ED=1:3,求BD的长.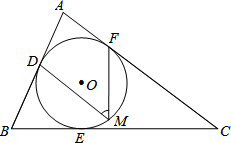 如图,⊙O是△ABC的内切圆,点D、E、F为切点,点M为优弧DEF上任意一点,∠B=66°,∠C=37°,求∠M的大小.
如图,⊙O是△ABC的内切圆,点D、E、F为切点,点M为优弧DEF上任意一点,∠B=66°,∠C=37°,求∠M的大小.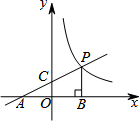 如图,直线y1=$\frac{1}{2}$x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y2=$\frac{k}{x}$(x>0)在第一象限内的交点,PB⊥x轴于点B,△PAB的面积为4.
如图,直线y1=$\frac{1}{2}$x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y2=$\frac{k}{x}$(x>0)在第一象限内的交点,PB⊥x轴于点B,△PAB的面积为4.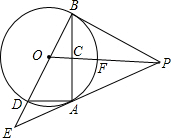 如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E.
如图,PA为⊙O的切线,A为切点.过A作OP的垂线AB,垂足为点C,交⊙O于点B.延长BO与⊙O交于点D,与PA的延长线交于点E. 某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示. 已知关于x的方程mx2-(3m-1)x+2m-2=0.
已知关于x的方程mx2-(3m-1)x+2m-2=0.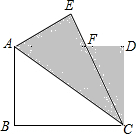 如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖的面积(阴影部分的面积)是29.25.
如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖的面积(阴影部分的面积)是29.25.