题目内容
1.在平行四边形ABCD中,∠ABC=60°,AB=2$\sqrt{3}$,AD=10,点P在直线BC上,且满足∠APD=90°,则∠APB的正切值为$\frac{1}{3}$或3.分析 作AM⊥BC于M,DN⊥BC于N,则∠AMP=∠DNP=90°,MN=AD=10,AM=DN,由平行四边形的性质和三角函数求出DN=AM=AB•sin60°=3,证明△PDN∽△APM,得出对应边成比例求出DN,即可得出结果.
解答 解:如图所示: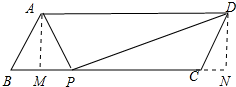
作AM⊥BC于M,DN⊥BC于N,
则∠AMP=∠DNP=90°,MN=AD=10,AM=DN,
∵四边形ABCD是平行四边形,
∴AB∥CD,CD=AB=2$\sqrt{3}$,
∵∠ABC=60°,
∴DN=AM=AB•sin60°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,
∵∠APD=90°,DN⊥BC,
∴∠PDN=∠APB,
∴△PDN∽△APM,
∴$\frac{PN}{AM}=\frac{DN}{PM}$,
即$\frac{PN}{3}=\frac{3}{10-PN}$,
解得:PN=1,或PN=9,
当PN=1时,tan∠APB=tan∠PDN=$\frac{PN}{DN}$=$\frac{1}{3}$;
当PN=1时,tan∠APB=tan∠PDN=$\frac{PN}{DN}$=3;
故答案为:$\frac{1}{3}$或3.
点评 本题考查了平行四边形的性质、三角函数、相似三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形相似得出PN的长是解决问题的关键.

练习册系列答案
相关题目
6.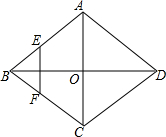 如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )
如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )
 如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )
如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | 7 |
5. 如图所示,将纸片△ABC沿着DE折叠压平,则( )
如图所示,将纸片△ABC沿着DE折叠压平,则( )
 如图所示,将纸片△ABC沿着DE折叠压平,则( )
如图所示,将纸片△ABC沿着DE折叠压平,则( )| A. | ∠A=∠1+∠2 | B. | ∠A=$\frac{1}{2}$(∠1+∠2) | C. | ∠A=$\frac{1}{3}$(∠1+∠2) | D. | ∠A=$\frac{1}{4}$(∠1+∠2) |
 如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是48cm,求:
如图,在菱形ABCD中,∠ABC与∠BAD的度数比为1:2,周长是48cm,求: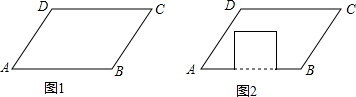
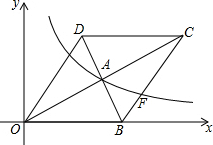 如图,在平面直角坐标系中.菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$的图象经过该菱形对角线的交点A,且与边BC交于点F,若点D的坐标为(6,8),求点F的坐标.
如图,在平面直角坐标系中.菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$的图象经过该菱形对角线的交点A,且与边BC交于点F,若点D的坐标为(6,8),求点F的坐标.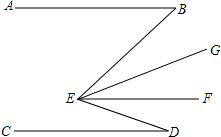 如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF=30°.
如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF=30°.