题目内容

6．计算：$\frac{3}{{a}^{2}-3a+2}$-$\frac{3}{5a-6-{a}^{2}}$=$\frac{6}{（a-1）（a-3）}$．

分析 先将两分式分母因式分解，确定最简公分母后通分，计算同分母分式相加，最后约分化简．

解答 解：原式=$\frac{3}{（a-1）（a-2）}$+$\frac{3}{（a-2）（a-3）}$
=$\frac{3（a-3）}{（a-1）（a-2）（a-3）}$+$\frac{3（a-1）}{（a-1）（a-2）（a-3）}$
=$\frac{3（a-3）+3（a-1）}{（a-1）（a-2）（a-3）}$
=$\frac{6（a-2）}{（a-1）（a-2）（a-3）}$
=$\frac{6}{（a-1）（a-3）}$．
故答案为：$\frac{6}{（a-1）（a-3）}$．

点评 本题主要考查分式的加减法运算，一般先将能因式分解的因式分解，再确定最简公分母，化成同分母分式依据法则计算化简即可．

练习册系列答案
相关题目
1．在平行四边形ABCD中，∠ABC=60°，AB=2$\sqrt{3}$，AD=10，点P在直线BC上，且满足∠APD=90°，则∠APB的正切值为$\frac{1}{3}$或3．
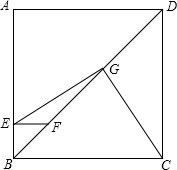17．已知正方形ABCD，点F为射线DB上一点，过点F作FE∥AD，FE交射线AB于E，G为FD的中点，连接CG，求证：∠CGE=90°．
14．解方程：$\frac{x}{2}$-$\frac{3-4x}{4}$=2-x-$\frac{5-3x}{8}$．
1．计算：$\frac{b-c}{{a}^{2}-ab-ac+bc}$-$\frac{c-a}{{b}^{2}-bc-ab+ac}$+$\frac{a-b}{{c}^{2}-ac-bc+ab}$．
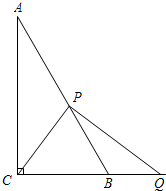11．如图，在Rt△ABC中，∠C=90°，AB=6，P是射线AB上的一个动点，PQ⊥PC，交线段CB的延长线于点Q．
（1）当BP=BC时，求证：BQ=BP；
（2）当点P在边AB上且∠A=30°时，设BP=x，BQ=y，求y关于x的函数解析式，并写出它的定义域；
（3）当∠A=30°，且BP=$\frac{5}{2}$时，请直接写出BQ的长．
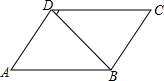18．已知：平行四边形ABCD，BD为对角线（如图）∠A=70°，∠BDC=30°，AD=15．求：∠C，∠ADB的度数，并求BC边的长．
15．若方程组$\left\{\begin{array}{l}{2{x}^{2}+m{y}^{{m}^{2}-2m-1}=2}\\{5{x}^{2}-3xy=4}\end{array}\right.$是二元二次方程组，求m的值．
16．若点A（x1，y1），B（x2，y2），和C（x3，y3），分别在反比例函数$y=\frac{6}{x}$的图象上，且x1＜x2＜0＜x3，则下列判断中正确的是（　　）
A．y1＜y2＜y3B．y2＜y1＜y3C．y3＜y2＜y1D．y2＜y3＜y1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网