题目内容
9.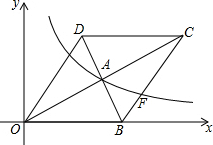 如图,在平面直角坐标系中.菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$的图象经过该菱形对角线的交点A,且与边BC交于点F,若点D的坐标为(6,8),求点F的坐标.
如图,在平面直角坐标系中.菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$的图象经过该菱形对角线的交点A,且与边BC交于点F,若点D的坐标为(6,8),求点F的坐标.
分析 首先过点D作DM⊥x轴于点M,过点F作FE⊥x于点E,由点D的坐标为(6,8),可求得菱形OBCD的边长,又由点A是BD的中点,求得点A的坐标,利用待定系数法即可求得反比例函数y=$\frac{k}{x}$(x>0)的解析式,然后由tan∠FBE=tan∠DOM=$\frac{DM}{OM}$=$\frac{4}{3}$,可设EF=4a,BE=3a,则点F的坐标为:(10+3a,4a),即可得方程4a(10+3a)=32,继而求得a的值,则可求得答案.
解答 解:过点D作DM⊥x轴于点M,过点F作FE⊥x于点E,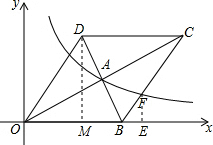
∵点D的坐标为(6,8),
∴OD=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵四边形OBCD是菱形,
∴OB=OD=10,
∴点B的坐标为:(10,0),
∵AB=AD,即A是BD的中点,
∴点A的坐标为:(8,4),
∵点A在反比例函数y=$\frac{k}{x}$上,
∴k=xy=8×4=32,
∵OD∥BC,
∴∠DOM=∠FBE,
∴tan∠FBE=tan∠DOM=$\frac{DM}{OM}$=$\frac{8}{6}$=$\frac{4}{3}$,
设EF=4a,BE=3a,
则点F的坐标为:(10+3a,4a),
∵点F在反比例函数y=$\frac{32}{x}$上,
∴4a(10+3a)=32,
即3a2+10a-8=0,
解得:a1=$\frac{2}{3}$,a2=-4(舍去),
∴点F的坐标为:(12,$\frac{8}{3}$).
点评 此题考查了菱形的性质、反比例函数的性质以及三角函数等知识.注意准确作出辅助线,求得反比例函数的解析式,得到tan∠FBE=tan∠DOM=$\frac{DM}{OM}$的值,从而得到方程4a(10+3a)=32是关键.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案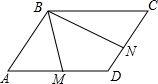 在?ABCD中,M是AD的中点,N是DC的中点,BM=1,BN=2,∠MBN=60°,求BC的长.
在?ABCD中,M是AD的中点,N是DC的中点,BM=1,BN=2,∠MBN=60°,求BC的长. 如图,三个全等的小矩形沿“横-竖-横”排列在一个边长分别为5.7,4.5的大矩形中,图中一个小矩形的周长等于6.8.
如图,三个全等的小矩形沿“横-竖-横”排列在一个边长分别为5.7,4.5的大矩形中,图中一个小矩形的周长等于6.8.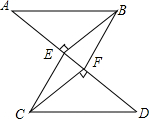 如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.