题目内容
15.已知二次函数y=x2+px+q图象的顶点M为直线y=$\frac{1}{2}$x+$\frac{1}{2}$与y=-x+m-1的交点.(1)用含m的代数式来表示顶点M的坐标(直接写出答案);
(2)当x≥2时,二次函数y=x2+px+q与y=$\frac{1}{2}$x+$\frac{1}{2}$的值均随x的增大而增大,求m的取值范围
(3)若m=6,当x取值为t-1≤x≤t+3时,二次函数y最小值=2,求t的取值范围.
分析 (1)已知直线y=$\frac{1}{2}$x+$\frac{1}{2}$和y=-x+m-1,列出方程求出x,y的等量关系式即可求出点M的坐标;
(2)根据题意得出$\frac{2m-3}{3}$≤2,解不等式求出m的取值;
(3)当t-1≤3时,当3≤t+3时,二次函数y最小值=2,解不等式组即可求得.
解答 解:(1)由$\left\{\begin{array}{l}{y=\frac{1}{2}x+\frac{1}{2}}\\{y=-x+m-1}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{x=\frac{2m-3}{3}}\\{y=\frac{m}{3}}\end{array}\right.$,
即交点M坐标为$(\frac{2m-3}{3},\frac{m}{3})$;
(2)∵二次函y=x2+px+q图象的顶点M为直线y=$\frac{1}{2}$x+$\frac{1}{2}$与y=-x+m-1的交点为$(\frac{2m-3}{3},\frac{m}{3})$,且当x≥2时,二次函数y=x2+px+q与y=$\frac{1}{2}$x+$\frac{1}{2}$的值均随x的增大而增大,
∴$\frac{2m-3}{3}$≤2,
解得m≤$\frac{9}{2}$,
∴m的取值范围为m≤$\frac{9}{2}$;
(3)∵m=6,
∴顶点为(3,2),
∴抛物线为y=(x-3)2+2,
∴函数y有最小值为2,
∵当x取值为t-1≤x≤t+3时,二次函数y最小值=2,
∴t-1≤3,t+3≥3,
解得0≤t≤4.
点评 此题主要考查了二次函数的性质以及图象,熟练掌握二次函数增减性是解题关键.

练习册系列答案
相关题目
6. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( )
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( )
 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( )
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( )| A. | $\frac{3}{5}$ | B. | $\frac{3\sqrt{13}}{13}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{13}}{13}$ |
3. 按要求用尺规作图,保留作图痕迹,不写作法
按要求用尺规作图,保留作图痕迹,不写作法
(1)请在图①的正方ABCD内,画出一个P满足∠APB=90°
(2)请在图②的正方ABCD内(含边),画出满足∠APB=90°的所有的P,并一句话说明理由.
 按要求用尺规作图,保留作图痕迹,不写作法
按要求用尺规作图,保留作图痕迹,不写作法(1)请在图①的正方ABCD内,画出一个P满足∠APB=90°
(2)请在图②的正方ABCD内(含边),画出满足∠APB=90°的所有的P,并一句话说明理由.
20.已知方程$\frac{3-a}{a-4}-1=\frac{9}{a-4}$,且关于x的不等式组$\left\{\begin{array}{l}{x>a}\\{x≤b}\end{array}\right.$只有4个整数解,那么b的取值范围是( )
| A. | -1<b≤3 | B. | 2<b≤3 | C. | 8≤b<9 | D. | 3≤b<4 |
4.若$\sqrt{\frac{y+2}{2x-1}}=\frac{{\sqrt{y+2}}}{{\sqrt{2x-1}}}$,且x+y=5,则x的取值范围是( )
| A. | x>$\frac{1}{2}$ | B. | $\frac{1}{2}$≤x<5 | C. | $\frac{1}{2}$<x<7 | D. | $\frac{1}{2}$<x≤7 |

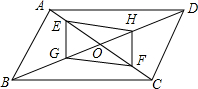 如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,AF=CE,BH=DG.求证:四边形EGFH是平行四边形.
如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,AF=CE,BH=DG.求证:四边形EGFH是平行四边形.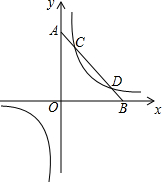 如图,已知点O为平面直角坐标系中的原点,点A在y轴正半轴上,点B在x轴正半轴上,OA=OB,线段AB和反比例函数y=$\frac{1}{x}$有两个不同的交点,分别是点C和点D,当$\frac{1}{4}$≤AC≤1时.线段CD的取值范围是1≤CD≤$\frac{31}{4}$.
如图,已知点O为平面直角坐标系中的原点,点A在y轴正半轴上,点B在x轴正半轴上,OA=OB,线段AB和反比例函数y=$\frac{1}{x}$有两个不同的交点,分别是点C和点D,当$\frac{1}{4}$≤AC≤1时.线段CD的取值范围是1≤CD≤$\frac{31}{4}$.