题目内容
4.若$\sqrt{\frac{y+2}{2x-1}}=\frac{{\sqrt{y+2}}}{{\sqrt{2x-1}}}$,且x+y=5,则x的取值范围是( )| A. | x>$\frac{1}{2}$ | B. | $\frac{1}{2}$≤x<5 | C. | $\frac{1}{2}$<x<7 | D. | $\frac{1}{2}$<x≤7 |
分析 直接利用二次根式有意义的条件,得出y的取值范围,进而得出答案.
解答 解:∵$\sqrt{\frac{y+2}{2x-1}}=\frac{{\sqrt{y+2}}}{{\sqrt{2x-1}}}$,
∴y+2≥0,2x-1>0,
解得:y≥-2,x>$\frac{1}{2}$,
∵x+y=5,
∴$\frac{1}{2}$<x≤7.
故选:D.
点评 此题主要考查了二次根式有意义的条件,得出y的取值范围是解题关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
12.在汶上县纪念抗日战争暨世界反法西斯战争胜利70周年歌咏比赛中,我校选手的得分情况如下:92,88,95,93,96,95,94.这组数据的众数和中位数分别是( )
| A. | 94,94 | B. | 95,95 | C. | 94,95 | D. | 95,94 |
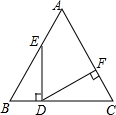 如图,在等边△ABC中,点D为BC边上的点,DE⊥BC交AB于E,DF⊥AC于F,则∠EDF的度数为60°.
如图,在等边△ABC中,点D为BC边上的点,DE⊥BC交AB于E,DF⊥AC于F,则∠EDF的度数为60°. 如图,已知点A(0,1),b(1,-1),C(3,3),将三角形ABC进行平移得到三角形A′B′C′.它内部的一点P(a,b)随之移到了点P(a-2,b-1),画出平移后的三角形A′B′C′,并写出三角形A′B′C′顶点的坐标.
如图,已知点A(0,1),b(1,-1),C(3,3),将三角形ABC进行平移得到三角形A′B′C′.它内部的一点P(a,b)随之移到了点P(a-2,b-1),画出平移后的三角形A′B′C′,并写出三角形A′B′C′顶点的坐标. 如图,在矩形ABCD中.AB=3,BC=4,沿EF折叠,折痕为EF,使C点落到A点处,点D落到G处.
如图,在矩形ABCD中.AB=3,BC=4,沿EF折叠,折痕为EF,使C点落到A点处,点D落到G处.