题目内容
7.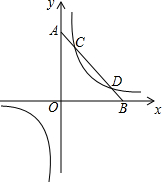 如图,已知点O为平面直角坐标系中的原点,点A在y轴正半轴上,点B在x轴正半轴上,OA=OB,线段AB和反比例函数y=$\frac{1}{x}$有两个不同的交点,分别是点C和点D,当$\frac{1}{4}$≤AC≤1时.线段CD的取值范围是1≤CD≤$\frac{31}{4}$.
如图,已知点O为平面直角坐标系中的原点,点A在y轴正半轴上,点B在x轴正半轴上,OA=OB,线段AB和反比例函数y=$\frac{1}{x}$有两个不同的交点,分别是点C和点D,当$\frac{1}{4}$≤AC≤1时.线段CD的取值范围是1≤CD≤$\frac{31}{4}$.
分析 作CE⊥y轴于E,根据题意易得△AOB和△AEC是等腰直角三角形,解直角三角形可全等C、D的坐标,然后根据勾股定理即可求得CD,从而求得取值范围.
解答 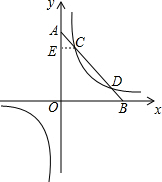 解:作CE⊥y轴于E,
解:作CE⊥y轴于E,
∵OA=OB,
∴△AOB和△AEC是等腰直角三角形,
当AC=$\frac{1}{4}$时,CE=$\frac{\sqrt{2}}{2}$AC=$\frac{\sqrt{2}}{2}$×$\frac{1}{4}$=$\frac{\sqrt{2}}{8}$,
∴C($\frac{\sqrt{2}}{8}$,4$\sqrt{2}$),
∴D(4$\sqrt{2}$,$\frac{\sqrt{2}}{8}$),
∴CD=$\sqrt{2(4\sqrt{2}-\frac{\sqrt{2}}{8})^{2}}$=$\frac{31}{4}$,
当AC=1时,CE=$\frac{\sqrt{2}}{2}$AC=$\frac{\sqrt{2}}{2}$,
∴C($\frac{\sqrt{2}}{2}$,$\sqrt{2}$),
∴D($\sqrt{2}$,$\frac{\sqrt{2}}{2}$),
∴CD=$\sqrt{2(\sqrt{2}-\frac{\sqrt{2}}{2})^{2}}$=1,
∴CD的取值范围是1≤CD≤$\frac{31}{4}$.
故答案为1≤CD≤$\frac{31}{4}$.
点评 本题考查了反比例函数与一次函数的交点,等腰直角三角形的性质以及勾股定理的应用,求得C、D的坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在汶上县纪念抗日战争暨世界反法西斯战争胜利70周年歌咏比赛中,我校选手的得分情况如下:92,88,95,93,96,95,94.这组数据的众数和中位数分别是( )
| A. | 94,94 | B. | 95,95 | C. | 94,95 | D. | 95,94 |
 如图,已知点A(0,1),b(1,-1),C(3,3),将三角形ABC进行平移得到三角形A′B′C′.它内部的一点P(a,b)随之移到了点P(a-2,b-1),画出平移后的三角形A′B′C′,并写出三角形A′B′C′顶点的坐标.
如图,已知点A(0,1),b(1,-1),C(3,3),将三角形ABC进行平移得到三角形A′B′C′.它内部的一点P(a,b)随之移到了点P(a-2,b-1),画出平移后的三角形A′B′C′,并写出三角形A′B′C′顶点的坐标.