题目内容
17.如图,在△ABC中,∠ACB=90°,AC=4,BC=3,点P在线段AB上以每秒1个单位的速度从点B向点A运动,同时点Q在线段AC上以同样的速度从点A向点C运动,运动的时间用t(单位:秒)表示.(1)直接写出线段AB的长为5;
(2)经过t秒时,AQ的长为t,AP的长为5-t(用含t的代数式表示);
(3)求当t为何值时,△APQ与△ABC相似?
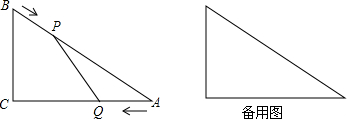
分析 (1)在Rt△ABC中,直接由勾股定理可得AB的长;
(2)由点P在线段AB上以每秒1个单位的速度从点B向点A运动可得经过t秒时,AQ的长为t,由同时点Q在线段AC上以同样的速度从点A向点C运动,可得BP=t,AP=5-t;
(3)由∠PAQ=∠BAC,利用相似三角形的SAS判定定理逆推可得当$\frac{AQ}{AC}=\frac{AP}{AB}$或$\frac{AP}{AC}=\frac{AQ}{AB}$△APQ与△ABC相似,利用(2)的结论,分两种情况讨论可得结果.
解答 解:(1)∵∠ACB=90°,AC=4,BC=3,
∴AB=$\sqrt{{AC}^{2}{+BC}^{2}}$=$\sqrt{{4}^{2}{+3}^{2}}$=5,
故答案为:5;
(2)∵点P在线段AB上以每秒1个单位的速度从点B向点A运动,
∴经过t秒时,AQ=t,
∵同时点Q在线段AC上以同样的速度从点A向点C运动,
∴BP=t,AP=5-t,
故答案为:t,5-t;
(3)∵∠PAQ=∠BAC,
∴当$\frac{AQ}{AC}=\frac{AP}{AB}$或$\frac{AP}{AC}=\frac{AQ}{AB}$△APQ与△ABC相似,
第一种情况,当$\frac{AQ}{AC}=\frac{AP}{AB}$时,
而AQ=t,AP=AB-BP=5-t,
∴$\frac{t}{4}=\frac{5-t}{5}$,
解得:$t=\frac{20}{9}$;
第二种情况,当$\frac{AP}{AC}=\frac{AQ}{AB}$时,
而AQ=t,AP=AB-BP=5-t,
∴$\frac{5-t}{4}=\frac{t}{5}$,
解得:$t=\frac{25}{9}$,
综上所述:当$t=\frac{20}{9}$或$t=\frac{25}{9}$时,△APQ与△ABC相似.
点评 本题主要考查了相似三角形的性质及判定定理,根据题意得出AQ,AP,利用SAS定理分两种情况讨论是解答此题的关键.

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
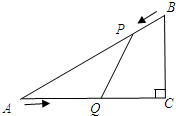 如图,已知在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:
如图,已知在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题: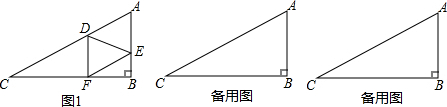
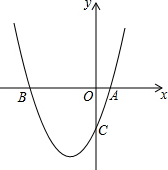 如图,已知抛物线y=x2+bx-3与x轴一个交点为A(1,0).
如图,已知抛物线y=x2+bx-3与x轴一个交点为A(1,0).