题目内容
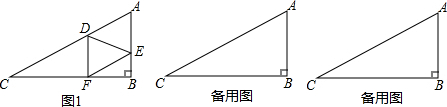
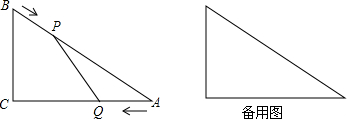
5.如图1,在Rt△ABC中,∠B=90°,∠C=30°,AC=6.动点D从C出发到A停止,沿线段CA以每秒1个单位长度的速度移动.先过点D作DF⊥BC于F,再过点F作FE∥AC,交AB于E.设动点D的运动时间为t秒.(1)填空:CD=t,DF=$\frac{1}{2}$t,(用含t的代数式表示)
(2)当四边形AEFD为菱形时,求t的值;
(3)当△FED是直角三角形时,求t的值.
分析 (1)利用已知D点运动速度与运动时间表示出DC的长,再利用锐角三角函数关系得出DF的长;
(2)利用菱形的性质结合(1)中所求即可得出答案;
(3)利用分类讨论结合①当∠DFE=90°时.②当∠FDE=90°时,③当∠DEF=90°时,分别分析得出符合题意的答案.
解答 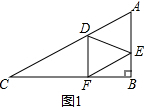 解:(1)∵动点D从C出发到A停止,沿线段CA以每秒1个单位长度的速度移动,过点D作DF⊥BC于F,
解:(1)∵动点D从C出发到A停止,沿线段CA以每秒1个单位长度的速度移动,过点D作DF⊥BC于F,
∴设动点D的运动时间为t秒,则CD=t,DF=CD•sin30°=$\frac{1}{2}$t,
故答案为:CD=t,DF=$\frac{1}{2}$t;
(2)如图1,当四边形AEFD为菱形时,有AD=DF,
∵AC=6,CD=t
∴AD=6-t,
∴6-t=$\frac{1}{2}$t,
∴t=4;
(3)讨论:
①当∠DFE=90°时.
∵FE∥AC,∠C=30°,
∴∠EFB=∠C=30°,
∴∠DFE=180°-90°-30°=60°≠90°,
∴这种情况不存在,
②当∠FDE=90°时,如图2,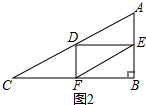
∵DF⊥BC,∠B=90°,
∴∠DFC=∠B=90°,
∴DF∥AB,
∵EF∥AC,
∴四边形AEFD为平行四边形,
∴AE=DF=$\frac{1}{2}t$,
∵∠DFC=∠FDE=90°,
∴∥BC,
∴∠ADE=∠C=30°,∠AED=∠B=90°,
在Rt△ADE中,∠AED=90°,∠ADE=30°,
∴AE=$\frac{1}{2}$AD,
即$\frac{1}{2}$t=$\frac{1}{2}$(6-t),
解得:t=3,
③当∠DEF=90°时,如图3,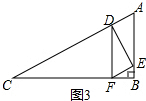
∵EF∥AC,∠C=30°,
∴∠EFB=∠C=30°,
∵∠EFC=90°,
∴∠DFE=60°,
∵∠DEF=90°,
∴∠FDE=30°,
∵∠B=90°,
∴∠FEB=60°,
∵∠DEF=90°,
∴∠AED=30°,
∴∠ADE=30°,
∴∠ADE=90°,∠AED=∠FDE=30°,
∴FD∥AE,
∴四边形AEFD为平行四边形,
∴AE=DF=$\frac{1}{2}$t,
在Rt△ADE中,
∠ADE=90°,∠AED=30°,
∴AD=$\frac{1}{2}$AE,
即6-t=$\frac{1}{2}$×$\frac{1}{2}$t,
解得:t=$\frac{24}{5}$.
综上所述,当△FED是直角三角形时,t的值为3或$\frac{24}{5}$.
点评 此题主要考查了四边形综合以及平行四边形的性质以及直角三角形的性质、菱形的判定等知识,根据题意结合分类讨论得出当△FED是直角三角形时求出t的值是解题关键.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案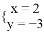 是二元一次方程4x+ay=7的一组解,则a的值为( )
是二元一次方程4x+ay=7的一组解,则a的值为( ) D.
D. 
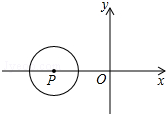 如图所示,在平面直角坐标系xOy中,半径为1的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为2或4.
如图所示,在平面直角坐标系xOy中,半径为1的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为2或4.
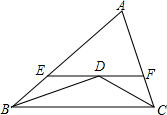 如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E,交AC于F.求证:EF=BE+CF.
如图所示,在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E,交AC于F.求证:EF=BE+CF.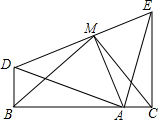 已知:如图,B、A、C三点共线,并且Rt△ABD≌Rt△ECA,M是DE的中点.
已知:如图,B、A、C三点共线,并且Rt△ABD≌Rt△ECA,M是DE的中点.