题目内容
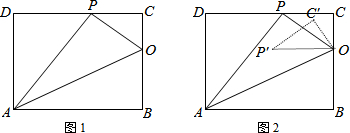
7.如图1,矩形ABCD中,AB=10,AD=8.将矩形ABCD折叠,使得顶点B落在CD边上的P点处.已知折痕AO与边BC交于点O,连结AP、OP、OA.(1)求OC的长;
(2)若将△PCO沿着射线PA方向平移,设平移的距离为n(平移距离指点P沿PA方向所经过的线段长度).当点C分别平移到线段PO、AO上时,直接写出相应的n的值;
(3)如图2,将△PCO绕点O逆时针旋转一个角α,记旋转中的△PCO为△P′OC′.在旋转过程中,设P′O所在的直线与线段AP交于点Q,与射线AD交于点H.是否存在这样的Q、H两点,使△AQH为等腰三角形?若存在,求出此时AQ的长;若不存在,请说明理由.
分析 (1)利用折叠和勾股定理求得答案即可;
(2)过C作CC1∥PA,交PO于C2,由此利用三角形的面积和折叠的性质求得答案即可;
(3)分三种情况探讨:①当QA=QH时,②当AH=AQ时,③当HA=HQ时,逐一分析探讨得出答案即可.
解答 解:(1)∵折叠,
∴AP=AB=10,AD=8,
∴DP=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴CP=4,
设OC=x,在直角三角形中,
(8-x)2=x2+42
解得:x=3
∴OC=3;
(2)如图1,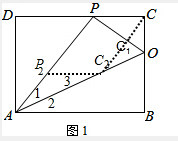
①过C作CC1∥PA,交PO于C2,
∵AP⊥PO,
∴CC1⊥PO,
∴CC1=$\frac{PC•CO}{PO}$=$\frac{12}{5}$=n;
②作P2C2∥AB,
则∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴AP2=P2C2=4,
∴PP2=10-4=n.
(3)①当QA=QH时,
∠DAQ=∠AHQ,
又∠AHQ=∠P′OC,
∵∠POC>∠DAP,
∴不存在.
②当AH=AQ时,
如图,
∵∠AQH=∠H,
∠H=∠QOC,
∴△EQO是等腰三角形,
∵∠EAB=∠APO,
∴tan∠EAB=$\frac{4}{3}$,
∴AE=$\frac{40}{3}$,
OE=$\frac{40}{3}$-5=$\frac{25}{3}$,
AE=$\frac{50}{3}$,
∴AQ=$\frac{50}{3}$-$\frac{25}{3}$=$\frac{25}{3}$.
③当HA=HQ时,
如图,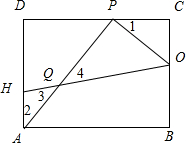
∠2=∠3.
又∵∠2=∠1,
∴∠1=∠4,
∵∠C=∠APO,
∴△PCO∽△QPO,
∴$\frac{PQ}{PC}$=$\frac{PO}{CO}$,
即PQ=$\frac{4×5}{3}$=$\frac{20}{3}$,
∴AQ=10-$\frac{20}{3}$=$\frac{10}{3}$.
点评 此题考查四边形的综合题,综合利用勾股定理,等腰三角形的性质,相似三角形的性质等知识解决问题,同时渗透分类讨论的思想.

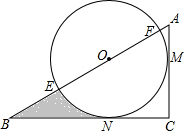 一个含30°角的三角尺与一张圆形硬纸片如图放置在桌面上,圆心O在斜边AB上,三角尺的两直角边与圆相切,切点分别为M、N.若AC=3+$\sqrt{3}$,则阴影部分的面积为( )
一个含30°角的三角尺与一张圆形硬纸片如图放置在桌面上,圆心O在斜边AB上,三角尺的两直角边与圆相切,切点分别为M、N.若AC=3+$\sqrt{3}$,则阴影部分的面积为( )| A. | 2$\sqrt{3}$-π | B. | $\sqrt{3}$-$\frac{1}{6}$π | C. | $\sqrt{3}$-$\frac{2}{3}$π | D. | $\frac{9\sqrt{3}}{2}$-$\frac{3}{2}$π |
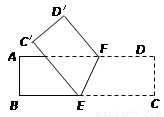
 如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )
如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
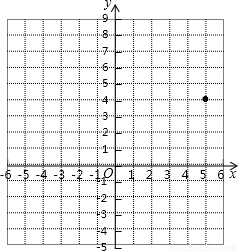
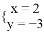 是二元一次方程4x+ay=7的一组解,则a的值为( )
是二元一次方程4x+ay=7的一组解,则a的值为( ) D.
D. 
 如图所示.长方形ABCD的周长是32cm,且5AD=3AB,把长方形ABCD绕直线AB旋转一周,然后用平面沿线段AB的方向截所得的几何体,求截面的最大面积.
如图所示.长方形ABCD的周长是32cm,且5AD=3AB,把长方形ABCD绕直线AB旋转一周,然后用平面沿线段AB的方向截所得的几何体,求截面的最大面积.