题目内容
16.已知线段x,y.(1)当$\frac{x+3y}{x-y}$=$\frac{3}{2}$时,求$\frac{x}{y}$的值;
(2)当$\frac{x+3y}{x-y}=\frac{x}{y}$时,求$\frac{x}{y}$的值.
分析 (1)由比例的性质对比例式进行变形,然后去括号、移项、合并同类项可得到x=9y;
(2)由比例的性质对比例式进行变形从而得到3y2+2xy-x2=0,然后分解得(3y-x)(y+x)=0.
解答 解:(1)由$\frac{x+3y}{x-y}$=$\frac{3}{2}$得:2(x+3y)=3(x-y),
去括号得:2x+6y=3x-3y,
移项、合并同类项得:9y=x,
∴$\frac{x}{y}=9$.
(2)由$\frac{x+3y}{x-y}=\frac{x}{y}$得:xy+3y2=x2-xy,
整理得:3y2+2xy-x2=0.
∴(3y-x)(y+x)=0.
∴3y-x=0或y+x=0.
∴$\frac{x}{y}=3$或$\frac{x}{y}=-1$(舍去).
∴$\frac{x}{y}$=3.
点评 本题主要考查的是比例的性质、因式分解、将3y2+2xy-x2=0分解为(3y-x)(y+x)=0是解题的关键.

练习册系列答案
相关题目
7.一条直线y=kx+b经过第二、三、四象限,则下列所给数据符合题意的是( )
| A. | k+b=6,kb=-5 | B. | k+b=-5,kb=-6 | C. | k+b=6,kb=5 | D. | k+b=-5,kb=6 |
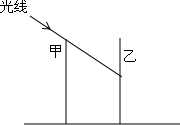 如图,甲、乙两楼的高都为30m,两楼相距24m,在某一时刻太阳光线与水平线的夹角为30°,则甲楼的影子落在乙楼上的高度为(30-8$\sqrt{3}$)m.
如图,甲、乙两楼的高都为30m,两楼相距24m,在某一时刻太阳光线与水平线的夹角为30°,则甲楼的影子落在乙楼上的高度为(30-8$\sqrt{3}$)m. 如图,AD是△ABC的边BC上的中线,若△ABD的周长比△ACD的周长小5,求AC与AB的差.
如图,AD是△ABC的边BC上的中线,若△ABD的周长比△ACD的周长小5,求AC与AB的差.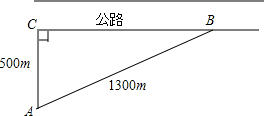 我方侦查员小王在距离东西向500米处公路侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距500米,30秒后,汽车与他相距1300米,请你帮小王计算敌方汽车的速度吗?
我方侦查员小王在距离东西向500米处公路侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距500米,30秒后,汽车与他相距1300米,请你帮小王计算敌方汽车的速度吗?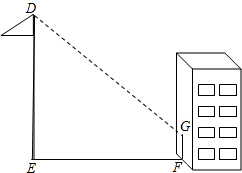 李明同学想利用影子测量旗杆的高度,他在某一时刻测得1m长的标杆影长为0.8m,当他测量教学楼前的旗杆的影长时,因旗杆靠近教学楼,有一部分影子在墙上,他测得旗杆到教学楼的距离EF=30m,旗杆在教学楼墙上的影长FG=1.5m,求旗杆DE的高.
李明同学想利用影子测量旗杆的高度,他在某一时刻测得1m长的标杆影长为0.8m,当他测量教学楼前的旗杆的影长时,因旗杆靠近教学楼,有一部分影子在墙上,他测得旗杆到教学楼的距离EF=30m,旗杆在教学楼墙上的影长FG=1.5m,求旗杆DE的高.