题目内容
4.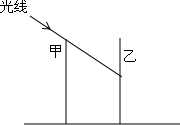 如图,甲、乙两楼的高都为30m,两楼相距24m,在某一时刻太阳光线与水平线的夹角为30°,则甲楼的影子落在乙楼上的高度为(30-8$\sqrt{3}$)m.
如图,甲、乙两楼的高都为30m,两楼相距24m,在某一时刻太阳光线与水平线的夹角为30°,则甲楼的影子落在乙楼上的高度为(30-8$\sqrt{3}$)m.
分析 过D作甲楼的垂线段DE,得到直角三角形ADE,则∠ADE=30°,DE=BC=24m,在这个三角形中已知一边和一个锐角,满足解直角三角形的条件,可求出AE的长从而求得BD的长.
解答 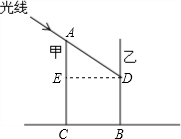 解:如图,过点D作DE⊥AC于E.
解:如图,过点D作DE⊥AC于E.
由题意可知∠ADE=30°,DE=BC=24m.
∵在Rt△ADE中,∠AED=90°,∠ADE=30°,DE=BC=24m,
∴在Rt△ADE中,tan∠ADE=$\frac{AE}{DE}$,
∴AE=DE•tan∠ADE=24•tan30°=8$\sqrt{3}$(m),
则DB=EC=AC-AE=30-8$\sqrt{3}$(m).
故答案为(30-8$\sqrt{3}$).
点评 本题考查了解直角三角形在生活中的实际应用,理清题意,正确的构造直角三角形是解答此题的关键.

练习册系列答案
相关题目
 如图所示,菱形ABCD的周长为32cm,菱形的相邻两内角之比为1:2,求菱形的面积.
如图所示,菱形ABCD的周长为32cm,菱形的相邻两内角之比为1:2,求菱形的面积. 如图,在一个高(BC)为6m,长(AC)为10m,宽为2.5m的楼梯表面铺地毯,若每平方米地毯50元,总共需要1750元.
如图,在一个高(BC)为6m,长(AC)为10m,宽为2.5m的楼梯表面铺地毯,若每平方米地毯50元,总共需要1750元. 如图,四边形ABCD中CD⊥DA,CE平分∠DCB交AD于E,AF平分∠DAB交BC于F,CE∥FA,求∠B.
如图,四边形ABCD中CD⊥DA,CE平分∠DCB交AD于E,AF平分∠DAB交BC于F,CE∥FA,求∠B.
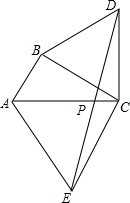 如图,△ABC中,∠ABC=90°,AC=2AB,△DBC与△AEC都是等边三角形,连结DE交AC于P,求证:PD=PE.
如图,△ABC中,∠ABC=90°,AC=2AB,△DBC与△AEC都是等边三角形,连结DE交AC于P,求证:PD=PE.