题目内容
6.⊙O的半径为8cm,弦AB的长为8$\sqrt{3}$cm,以O为圆心,4cm为半径作圆,与弦AB有1个公共点.分析 根据垂径定理求出AC的长,根据勾股定理求出OC的长,根据直线与圆的关系公式得到答案.
解答 解: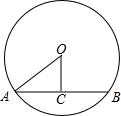 ∵OC⊥AB,
∵OC⊥AB,
∴AC=$\frac{1}{2}$AB=4$\sqrt{3}$,
∴OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=4,
∴以O为圆心,4cm为半径作圆,与弦AB相切,
则公共点只有一个,
故答案为:1.
点评 本题考查的是直线与圆的关系和垂径定理的应用,掌握圆心到直线的距离等于圆的半径时,直线与圆相切是解题的关键.

练习册系列答案
相关题目
18.如图,下列四个几何体,从上面、正面、左侧三个不同方向看到的形状中只有两个相同的是( )
| A. |  正方体 | B. |  球 | C. |  直三棱柱 | D. |  圆柱 |
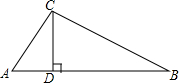 如图所示,在△ABC中,∠A为锐角,CD为AB边上的高,$\frac{CD}{AC}$=$\frac{3}{5}$,AB+AC=6,设AC=x,△ABC的面积为y.
如图所示,在△ABC中,∠A为锐角,CD为AB边上的高,$\frac{CD}{AC}$=$\frac{3}{5}$,AB+AC=6,设AC=x,△ABC的面积为y.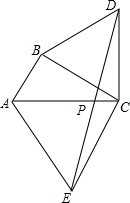 如图,△ABC中,∠ABC=90°,AC=2AB,△DBC与△AEC都是等边三角形,连结DE交AC于P,求证:PD=PE.
如图,△ABC中,∠ABC=90°,AC=2AB,△DBC与△AEC都是等边三角形,连结DE交AC于P,求证:PD=PE.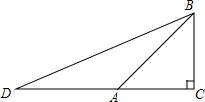 如图,在△ABC中,∠C=90°,AC=BC,延长CA到D使AD=AB,
如图,在△ABC中,∠C=90°,AC=BC,延长CA到D使AD=AB,