题目内容
8.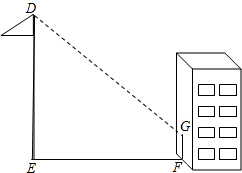 李明同学想利用影子测量旗杆的高度,他在某一时刻测得1m长的标杆影长为0.8m,当他测量教学楼前的旗杆的影长时,因旗杆靠近教学楼,有一部分影子在墙上,他测得旗杆到教学楼的距离EF=30m,旗杆在教学楼墙上的影长FG=1.5m,求旗杆DE的高.
李明同学想利用影子测量旗杆的高度,他在某一时刻测得1m长的标杆影长为0.8m,当他测量教学楼前的旗杆的影长时,因旗杆靠近教学楼,有一部分影子在墙上,他测得旗杆到教学楼的距离EF=30m,旗杆在教学楼墙上的影长FG=1.5m,求旗杆DE的高.
分析 过点G作GH∥EF交DE于H,根据同时同地物高与影长成正比求出DH,再根据DE=DH+EH计算即可得解.
解答  解:如图,过点G作GH∥EF交DE于H,
解:如图,过点G作GH∥EF交DE于H,
则四边形EFGH是矩形,
所以,GH=EF=30m,EH=FG=1.5m,
由题意得,$\frac{DH}{GH}$=$\frac{1}{0.8}$,
所以$\frac{DH}{30}$=$\frac{1}{0.8}$,
解得DH=37.5m,
所以DE=DH+EH=37.5+1.5=39m.
答:旗杆DE的高是39m.
点评 本题考查了相似三角形的应用,主要利用了同时同地物高与影长成正比,难点在于作辅助线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.如图,下列四个几何体,从上面、正面、左侧三个不同方向看到的形状中只有两个相同的是( )
| A. |  正方体 | B. |  球 | C. |  直三棱柱 | D. |  圆柱 |
 如图,在一个高(BC)为6m,长(AC)为10m,宽为2.5m的楼梯表面铺地毯,若每平方米地毯50元,总共需要1750元.
如图,在一个高(BC)为6m,长(AC)为10m,宽为2.5m的楼梯表面铺地毯,若每平方米地毯50元,总共需要1750元.

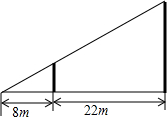 如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m、与旗杆相距22m,求旗杆的高度.
如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m、与旗杆相距22m,求旗杆的高度.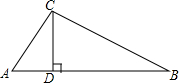 如图所示,在△ABC中,∠A为锐角,CD为AB边上的高,$\frac{CD}{AC}$=$\frac{3}{5}$,AB+AC=6,设AC=x,△ABC的面积为y.
如图所示,在△ABC中,∠A为锐角,CD为AB边上的高,$\frac{CD}{AC}$=$\frac{3}{5}$,AB+AC=6,设AC=x,△ABC的面积为y.