题目内容
13. 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)作图:在△BED中作BD边上的高,垂足为F;
(3)若△ABC的面积为60,BD=6,则△BDE中BD边上的高为多少?
分析 (1)直接根据三角形外角的性质即可得出结论;
(2)过点E作EF⊥BC,垂足为F即可;
(3)先求出△BDE的面积,再由三角形的面积公式即可得出结论.
解答  解:(1)在△ABE中,
解:(1)在△ABE中,
∵∠ABE=15°,∠BAD=40°,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
(2)如图,EF即为所求;
(3)∵△ABC的面积为60,AD为△ABC的中线,
∴S△ABD=$\frac{1}{2}$S△ABC=30.
∵BE为△ABD的中线,
∴S△BDE=$\frac{1}{2}$S△ABD=15.
∵BD=6,EF⊥BC,
∴$\frac{1}{2}$BD•EF=15,即$\frac{1}{2}$×6EF=15,解得EF=5.
点评 本题考查的是基本作图及三角形的面积、三角形的中线等知识,熟知三角形的中线将三角形分为面积相等的两部分是解答此题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
3.若关于x的一元二次方程ax2-bx+4=0的解是x=2,则2017+2a-b=( )
| A. | 2015 | B. | 2017 | C. | 2019 | D. | 2020 |
 某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.
某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.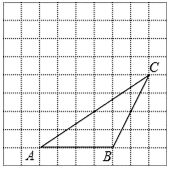 如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的△A′B′C′,再在图中画出△A′B′C′的高C′D′、中线A′E,若S△BCP=S△ACB,P为异于点B的格点,则点P的个数为4个.
如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的△A′B′C′,再在图中画出△A′B′C′的高C′D′、中线A′E,若S△BCP=S△ACB,P为异于点B的格点,则点P的个数为4个.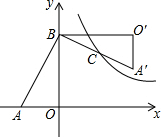 如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=$\frac{k}{x}$的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=6.
如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=$\frac{k}{x}$的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=6.