题目内容
2.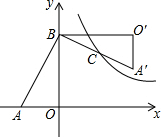 如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=$\frac{k}{x}$的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=6.
如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=$\frac{k}{x}$的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=6.
分析 先根据S△ABO=4,tan∠BAO=2求出AO、BO的长度,再根据点C为斜边A′B的中点,求出点C的坐标,点C的横纵坐标之积即为k值.
解答 解:设点C坐标为(x,y),作CD⊥BO′交边BO′于点D,
∵tan∠BAO=2,
∴$\frac{BO}{AO}$=2,
∵S△ABO=$\frac{1}{2}$•AO•BO=4,
∴AO=2,BO=4,
∵△ABO≌△A'O'B,
∴AO=A′O′=2,BO=BO′=4,
∵点C为斜边A′B的中点,CD⊥BO′,
∴CD=$\frac{1}{2}$A′O′=1,BD=$\frac{1}{2}$BO′=2,
∴x=BO-CD=4-1=3,y=BD=2,
∴k=x•y=3•2=6.
故答案为6.
点评 本题考查了反比例函数图象上点的坐标特征,解答本题的关键在于读懂题意,作出合适的辅助线,求出点C的坐标,然后根据点C的横纵坐标之积等于k值求解即可.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
7.下列水平放置的几何体中,俯视图是矩形的是( )
| A. |  | B. |  | C. |  | D. |  |
14. 三本相同的书本叠成如图所示的几何体,它的俯视图是( )
三本相同的书本叠成如图所示的几何体,它的俯视图是( )
 三本相同的书本叠成如图所示的几何体,它的俯视图是( )
三本相同的书本叠成如图所示的几何体,它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
12.下列命题是真命题的是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是正方形 | |
| C. | 一组对边平行的四边形是平行四边形 | |
| D. | 四边相等的四边形是菱形 |
 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.