��Ŀ����
1���Ķ��������ϣ�$\frac{1}{1+\sqrt{2}}$=$\frac{1����\sqrt{2}-1��}{��\sqrt{2}+1����\sqrt{2}-1��}$=$\sqrt{2}$-1��
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{��\sqrt{3}+\sqrt{2}����\sqrt{3}-\sqrt{2}��}$=$\sqrt{3}$-$\sqrt{2}$��
$\frac{1}{\sqrt{5}+2}$=$\frac{\sqrt{5}-2}{��\sqrt{5}+2����\sqrt{5}-2��}$=$\sqrt{5}$-2��
����1��$\frac{1}{\sqrt{7}+\sqrt{6}}$��ֵ��
��2��$\frac{1}{3\sqrt{2}+\sqrt{17}}$��ֵ��
��3����$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+��+$\frac{1}{\sqrt{2008}+\sqrt{2009}}$+$\frac{1}{\sqrt{2009}+\sqrt{2010}}$��•��1+$\sqrt{2010}$����
���� ��1��ԭʽ�����Ķ������еķ������ֵ���ɣ�
��2��ԭʽ�����Ķ������еķ������ֵ���ɣ�
��3��ԭʽ��һ�������з����Ķ������еķ������Σ����㼴�ɵõ������
��� �⣺��1��ԭʽ=$\frac{\sqrt{7}-\sqrt{6}}{��\sqrt{7}+\sqrt{6}����\sqrt{7}-\sqrt{6}��}$=$\sqrt{7}$-$\sqrt{6}$��
��2��ԭʽ=$\frac{3\sqrt{2}-\sqrt{17}}{��3\sqrt{2}+\sqrt{17}����3\sqrt{2}-\sqrt{17}��}$=3$\sqrt{2}$-$\sqrt{17}$��
��3��ԭʽ=��$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+��+$\sqrt{2009}$-$\sqrt{2008}$+$\sqrt{2010}$-$\sqrt{2009}$��•��1+$\sqrt{2010}$��
=��$\sqrt{2010}$-1����$\sqrt{2010}$+1��
=2010-1
=2009��
���� ���⿼���˷�ĸ��������Ū���Ķ������еķ����ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
11���ڡ�ABC�У�AB=13��BC=10��BC���ϵ�����AD=12����AC=��������
| A�� | 10 | B�� | 11 | C�� | 12 | D�� | 13 |
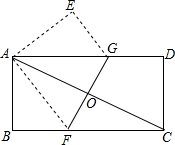 ��ͼ����һ����ֽƬABCD�۵���ʹ��������A��C�غϣ��ۺ�ΪFG..��AB=8��BC=16�����AEG�����Ϊ24��
��ͼ����һ����ֽƬABCD�۵���ʹ��������A��C�غϣ��ۺ�ΪFG..��AB=8��BC=16�����AEG�����Ϊ24�� ��ͼ��ADΪ��ABC�����ߣ�BEΪ��ABD�����ߣ�
��ͼ��ADΪ��ABC�����ߣ�BEΪ��ABD�����ߣ�