题目内容
8. 某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.
某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.(参考数据:sin37°=cos53°≈$\frac{3}{5}$,cos37°=sin53°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$)
分析 作AH⊥CD于H,作CF⊥AB于F,在Rt△AHD中利用三角函数求得DH的长,在Rt△BCF中利用三角函数求得BF的长,则AB的长即可求得.
解答  解:作AH⊥CD于H,作CF⊥AB于F,
解:作AH⊥CD于H,作CF⊥AB于F,
在Rt△AHD中,∠ADH=37°,由sin37°=$\frac{AH}{AD}$,得AD=8.5(m),
由tan37°=$\frac{AH}{DH}$,得DH=$\frac{AH}{tan37°}$=$\frac{5.1}{\frac{3}{4}}$=6.8(m),
Rt△BCF中,∠CBF=45°,BF=CF=5.1m,
∵AB+BF=HD+DC,
∴AB=6.8+1.4-5.1=3.1(m).
点评 此题考查了解直角三角形的应用,解答本题的关键是构建直角三角形,将实际问题转化为数学模型,难度一般.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
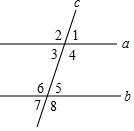 如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6②∠1=∠7③∠1+∠4=180°④∠3=∠8,其中能推断a∥b的条件的序号是( )
如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6②∠1=∠7③∠1+∠4=180°④∠3=∠8,其中能推断a∥b的条件的序号是( )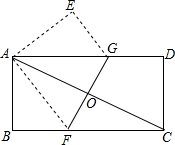 如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG..若AB=8,BC=16,则△AEG的面积为24.
如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG..若AB=8,BC=16,则△AEG的面积为24.
 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.