题目内容
4.Rt△ABC中,∠C=90°,AC=6,BC=8,如果以点C为圆心,r为半径,且⊙C与斜边AB仅有一个公共点,那么半径r的取值范围是r=4.8或6<r≤8.分析 因为要使圆与斜边只有一个公共点,所以该圆和斜边相切或和斜边相交,但只有一个交点在斜边上.
若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
解答 解:根据勾股定理求得直角三角形的斜边AB=$\sqrt{{8}^{2}+{6}^{2}}$=10,
当圆和斜边相切时,则半径即是斜边上的高,等于$\frac{24}{5}$;
当圆和斜边相交,且只有一个交点在斜边上时,可以让圆的半径大于短直角边而小于长直角边,则6<r≤8.
故半径r的取值范围是r=4.8或6<r≤8.
故答案为:r=4.8或6<r≤8.
点评 此题考查了直线与圆的位置关系,此题注意考虑两种情况,只需保证圆和斜边只有一个公共点即可.

练习册系列答案
相关题目
14. 三本相同的书本叠成如图所示的几何体,它的俯视图是( )
三本相同的书本叠成如图所示的几何体,它的俯视图是( )
 三本相同的书本叠成如图所示的几何体,它的俯视图是( )
三本相同的书本叠成如图所示的几何体,它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
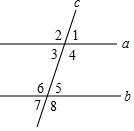 如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6②∠1=∠7③∠1+∠4=180°④∠3=∠8,其中能推断a∥b的条件的序号是( )
如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6②∠1=∠7③∠1+∠4=180°④∠3=∠8,其中能推断a∥b的条件的序号是( )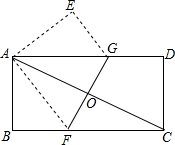 如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG..若AB=8,BC=16,则△AEG的面积为24.
如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG..若AB=8,BC=16,则△AEG的面积为24. 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.