题目内容
15. 如图在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.
如图在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.(1)求证:ED是⊙O的切线;
(2)如果⊙O的半径为1.5,ED=2,求AB的长.
(3)在(2)的条件下,延长EO交⊙O于F,连接DF、AF,求s的面积.
分析 (1)先由OA=OD得出∠BAC=∠ADO,再由OE∥AB得出∠COE=∠BAC,∠DOE=∠ADO,进而得出∠COE=∠DOE,即可判断出△COE≌△DOE(SAS)得到∠ODE=∠C=90°,即可;
(2)由(1)得出△COE≌△DOE(SAS),得出CE=DE=2,用勾股定理求出OE,再判断出OE是△ABC的中位线,即可求出AB;
(3)先判断出OE垂直平分CD,再用△COE的面积求出斜边上的高,进而得出CD,用勾股定理求出AD,最后用三角形的面积公式即可得出结论.
解答 解:(1)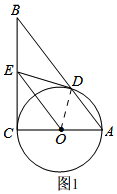 连接OD,
连接OD,
∵OA=OD,
∴∠BAC=∠ADO,
∵OE∥AB,
∴∠COE=∠BAC,∠DOE=∠ADO,
∴∠COE=∠DOE,
在△COE和△DOE中,$\left\{\begin{array}{l}{OC=OD}\\{∠COE=∠DOE}\\{OE=OE}\end{array}\right.$,
∴△COE≌△DOE(SAS),
∴∠C=∠ODE,
∵∠C=90°,
∴∠ODE=∠C=90°,
∵点D在⊙O上,
∴ED是⊙O的切线;
(2)由(1)知,△COE≌△DOE(SAS),
∴CE=DE=2,
在Rt△OCE中,OC=1.5,CE=2,
根据勾股定理得,OE=$\sqrt{O{C}^{2}+C{E}^{2}}$=$\frac{5}{2}$,
∵OE∥AB,OA=OC,
∴OE是△ABC的中位线,
∴AB=2OE=5;
(3)如图2,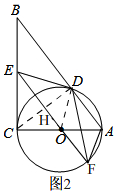 连接CD交OE于H,连接OD,
连接CD交OE于H,连接OD,
由(1)知,∠COE=∠DOE,
∵OC=OD,
∴OE⊥CD,DH=CH=$\frac{1}{2}$CD,
在Rt△OCE中,OC=1.5,CE=2,OE=$\frac{5}{2}$,
∵S△OCE=$\frac{1}{2}$OC•CE=$\frac{1}{2}$OE•CH,
∴CH=$\frac{OC•CE}{OE}$=$\frac{6}{5}$,
∴DH=$\frac{6}{5}$,CD=2CH=$\frac{12}{5}$,
∵AC是⊙O的直径,
∴∠ADC=90°,
在Rt△ACD中,CD=$\frac{12}{5}$,AC=2OA=3,
根据勾股定理得,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\frac{9}{5}$,
∵OE∥AB,
∴△ADF的边上的高h和DH相等,
∴h=DH=$\frac{6}{5}$,
∴S△ADF=$\frac{1}{2}$AD•h=$\frac{1}{2}$×$\frac{9}{5}$×$\frac{6}{5}$=$\frac{27}{25}$.
点评 此题是圆的综合题,主要考查了切线的判定,全等三角形的判断和性质,勾股定理,垂径定理,判断出△COE≌△DOE(SAS)和求出CH是解本题的关键,是一道中等难度的中考常考题.

| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | |
| 售价x(元/千克) | 18 | 15 | 12 | 10 | 9 |
| 销售量y(千克) | 50 | 60 | 75 | 90 | 100 |
(2)在试销5天后,该农户决定将这批樱桃的售价定为12元/千克,求剩余的樱桃预计还要多少天才可以全部售完?
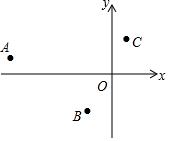 在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点A,B,C,则对系数a和b判断正确的是( )
在平面直角坐标系xOy中,二次函数y=ax2+bx的图象经过点A,B,C,则对系数a和b判断正确的是( )| A. | a>0,b>0 | B. | a<0,b<0 | C. | a>0,b<0 | D. | a<0,b>0 |
 已知△ABC分别以△ABC的AC,BC边为腰,A,B为直角顶点,作等腰Rt△ACE和等腰Rt△BCD,M为ED的中点,求证:AM⊥BM.
已知△ABC分别以△ABC的AC,BC边为腰,A,B为直角顶点,作等腰Rt△ACE和等腰Rt△BCD,M为ED的中点,求证:AM⊥BM. 作图:已知∠AOB,试在∠AOB内确定一点P,使P到OA、OB的距离相等,并且到M、N两点的距离也相等.
作图:已知∠AOB,试在∠AOB内确定一点P,使P到OA、OB的距离相等,并且到M、N两点的距离也相等. 已知:如图,△ABC.
已知:如图,△ABC.