题目内容
4．
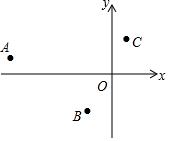在平面直角坐标系xOy中，二次函数y=ax2+bx的图象经过点A，B，C，则对系数a和b判断正确的是（ ）| A． | a＞0，b＞0 | B． | a＜0，b＜0 | C． | a＞0，b＜0 | D． | a＜0，b＞0 |
分析 根据二次函数y=ax2+bx的图象经过点A，B，C，画出函数图象的草图，根据开口方向和对称轴即可判断．
解答 解：由题意知，二次函数y=ax2+bx的图象经过点A，B，C，
则函数图象如图所示，
∴a＞0，-$\frac{b}{2a}$＜0，
∴b＞0，
故选：A．
点评 题考查了二次函数的图象与性质、不等式的性质，利用数形结合是解题的关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图，在△AOB中，OA=OB，∠AOB=50°，将△AOB绕O点顺时针旋转30°，得到△COD，OC交AB于点F，CD分别交AB、OB于点E、H．求证：EF=EH．
如图在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过O作OE∥AB，交BC于E．
12．
如图，直线m同侧有A、B两点，A、A′关于直线m对称，A、B关于直线n对称，直线m与A′B和n分别交于P、Q，下面的说法正确的是（ ）
如图，直线m同侧有A、B两点，A、A′关于直线m对称，A、B关于直线n对称，直线m与A′B和n分别交于P、Q，下面的说法正确的是（ ）| A． | P是m上到A、B距离之和最短的点，Q是m上到A、B距离相等的点 | |
| B． | Q是m上到A、B距离之和最短的点，P是m上到A、B距离相等的点 | |
| C． | P、Q都是m上到A、B距离之和最短的点 | |
| D． | P、Q都是m上到A、B距离相等的点 |
19．解方程：
（1）$\frac{1}{x+1}$+$\frac{2}{x-1}$=$\frac{4}{{{x^2}-1}}$
（2）$\frac{3}{x-2}$=$\frac{x}{2-x}$-2．
（1）$\frac{1}{x+1}$+$\frac{2}{x-1}$=$\frac{4}{{{x^2}-1}}$
（2）$\frac{3}{x-2}$=$\frac{x}{2-x}$-2．
16．二次函数 y=ax2+bx+c 的部分自变量和对应函数值如下：
当 x=3 时，y=-4．
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -6.5 | -4 | -2.5 | -2 | -2.5 | … |