题目内容
6.计算:①8+(-10)+(-2)-(-5)
②(-3$\frac{2}{3}$)-(-2$\frac{3}{4}$)-(-1$\frac{2}{3}$)-(+1.75)
③8×(-$\frac{4}{5}$)÷|-16|
④-14-[-3×(-$\frac{2}{3}$)2-1$\frac{1}{3}$÷(-2)2]
⑤-52×(-$\frac{3}{5}$)-32÷(-2)2×(+1$\frac{1}{4}$)
⑥(-8)×$\frac{3}{16}$-(-14)÷7.
分析 ①原式利用减法法则变形,计算即可得到结果;
②原式利用减法法则变形,计算即可得到结果;
③原式从左到右依次计算即可得到结果;
④原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
⑤原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
⑥原式先计算乘除运算,再计算加减运算即可得到结果.
解答 解:①原式=8-10-2+5=13-12=1;
②原式=-3$\frac{2}{3}$+1$\frac{2}{3}$+2$\frac{3}{4}$-1.75=-2+1=-1;
③原式=-8×$\frac{4}{5}$×$\frac{1}{16}$=-10;
④原式=-1+$\frac{4}{3}$+$\frac{1}{3}$=$\frac{2}{3}$;
⑤原式=15-10=5;
⑥原式=-$\frac{3}{2}$+2=$\frac{1}{2}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.二次函数 y=ax2+bx+c 的部分自变量和对应函数值如下:
当 x=3 时,y=-4.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -6.5 | -4 | -2.5 | -2 | -2.5 | … |
 如图,在△AOB中,OA=OB,∠AOB=50°,将△AOB绕O点顺时针旋转30°,得到△COD,OC交AB于点F,CD分别交AB、OB于点E、H.求证:EF=EH.
如图,在△AOB中,OA=OB,∠AOB=50°,将△AOB绕O点顺时针旋转30°,得到△COD,OC交AB于点F,CD分别交AB、OB于点E、H.求证:EF=EH.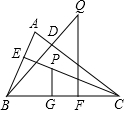 已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.
已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.
 如图在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.
如图在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.