题目内容
12.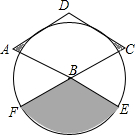 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )| A. | $\sqrt{3}$+$\frac{π}{2}$ | B. | $\sqrt{3}$+π | C. | $\sqrt{3}$-$\frac{π}{2}$ | D. | 2$\sqrt{3}$+$\frac{π}{2}$ |
分析 设AD与圆的切点为G,连接BG,通过解直角三角形求得圆的半径,然后根据扇形的面积公式求得三个扇形的面积,进而就可求得阴影的面积.
解答 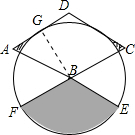 解:设AD与圆的切点为G,连接BG,
解:设AD与圆的切点为G,连接BG,
∴BG⊥AD,
∵∠A=60°,BG⊥AD,
∴∠ABG=30°,
在直角△ABG中,BG=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$,AG=1,
∴圆B的半径为$\sqrt{3}$,
∴S△ABG=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$
在菱形ABCD中,∠A=60°,则∠ABC=120°,
∴∠EBF=120°,
∴S阴影=2(S△ABG-S扇形)+S扇形FBE=2($\frac{\sqrt{3}}{2}$-$\frac{30π×3}{360}$)+$\frac{120×π×(\sqrt{3})^{2}}{360}$=$\sqrt{3}$+$\frac{π}{2}$.
故选A.
点评 此题主要考查了菱形的性质以及切线的性质以及扇形面积等知识,正确利用菱形的性质和切线的性质求出圆的半径是解题关键.

练习册系列答案
相关题目
3. 如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是( )
如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是( )
 如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是( )
如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是( )| A. | $\sqrt{7}$ | B. | $\sqrt{7}-1$ | C. | $\sqrt{3}$ | D. | 2 |
7.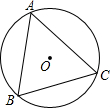 如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
 如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )| A. | 4$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 8 |
4. 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )
 如图所示的几何体的俯视图是( )
如图所示的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
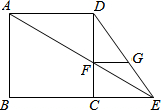 如图,点E为正方形ABCD边延长线上一点,AE交CD于F点,FG∥AD交DE于G点,其中有△ABE∽△FCE,△EFG∽△EAD,请探求CF与FG的大小关系,并说明理由.
如图,点E为正方形ABCD边延长线上一点,AE交CD于F点,FG∥AD交DE于G点,其中有△ABE∽△FCE,△EFG∽△EAD,请探求CF与FG的大小关系,并说明理由.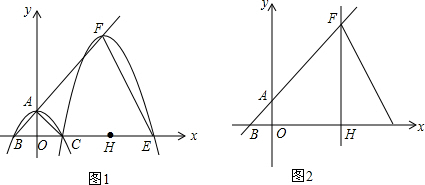
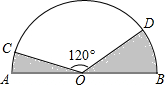 如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于$\frac{2}{3}$π.
如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于$\frac{2}{3}$π. 如图,?ABCD中,点E,F在对角线BD上,且BE=DF,求证:
如图,?ABCD中,点E,F在对角线BD上,且BE=DF,求证: