题目内容
1.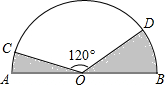 如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于$\frac{2}{3}$π.
如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于$\frac{2}{3}$π.
分析 图中阴影部分的面积=半圆的面积-圆心角是120°的扇形的面积,根据扇形面积的计算公式计算即可求解.
解答 解:图中阴影部分的面积=$\frac{1}{2}$π×22-$\frac{120×π×{2}^{2}}{360}$
=2π-$\frac{4}{3}$π
=$\frac{2}{3}$π.
答:图中阴影部分的面积等于$\frac{2}{3}$π.
故答案为:$\frac{2}{3}$π.
点评 考查了扇形面积的计算,求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积.

练习册系列答案
相关题目
12.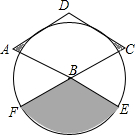 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )| A. | $\sqrt{3}$+$\frac{π}{2}$ | B. | $\sqrt{3}$+π | C. | $\sqrt{3}$-$\frac{π}{2}$ | D. | 2$\sqrt{3}$+$\frac{π}{2}$ |
13.下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律排列,则第⑦个图形中小圆圈的个数为( )


| A. | 21 | B. | 24 | C. | 27 | D. | 30 |
10.在正方形、矩形、菱形、平行四边形、等腰梯形中,其中中心对称图形的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11.下列运算中,正确的是( )
| A. | x3+x=x4 | B. | (x2)3=x6 | C. | 3x-2x=1 | D. | (a-b)2=a2-b2 |
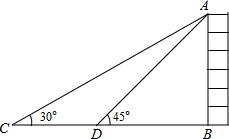 如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.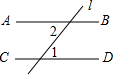 如图,AB∥CD,直线l分别与AB,CD相交,若∠1=50°,则∠2的度数为50°.
如图,AB∥CD,直线l分别与AB,CD相交,若∠1=50°,则∠2的度数为50°.