题目内容
2. 如图,?ABCD中,点E,F在对角线BD上,且BE=DF,求证:
如图,?ABCD中,点E,F在对角线BD上,且BE=DF,求证:(1)AE=CF;
(2)四边形AECF是平行四边形.
分析 (1)根据平行四边形的性质可得AB=CD,AB∥CD,然后可证明∠ABE=∠CDF,再利用SAS来判定△ABE≌△DCF,从而得出AE=CF.
(2)首先根据全等三角形的性质可得∠AEB=∠CFD,根据等角的补角相等可得∠AEF=∠CFE,然后证明AE∥CF,从而可得四边形AECF是平行四边形.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
$\left\{\begin{array}{l}{AB=CD}\\{∠ABE=∠CDF}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△DCF(SAS).
∴AE=CF.
(2)∵△ABE≌△DCF,
∴∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
点评 此题主要考查了平行四边形的性质和判定,关键是掌握平行四边形对边平行且相等,一组对边平行且相等的四边形是平行四边形.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
12.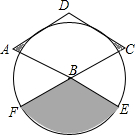 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )| A. | $\sqrt{3}$+$\frac{π}{2}$ | B. | $\sqrt{3}$+π | C. | $\sqrt{3}$-$\frac{π}{2}$ | D. | 2$\sqrt{3}$+$\frac{π}{2}$ |
13.下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律排列,则第⑦个图形中小圆圈的个数为( )


| A. | 21 | B. | 24 | C. | 27 | D. | 30 |
10.在正方形、矩形、菱形、平行四边形、等腰梯形中,其中中心对称图形的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
14.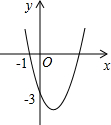 如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )
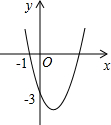 如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)过点(-1,0)和点(0,-3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )| A. | -3<P<-1 | B. | -6<P<0 | C. | -3<P<0 | D. | -6<P<-3 |
11.下列运算中,正确的是( )
| A. | x3+x=x4 | B. | (x2)3=x6 | C. | 3x-2x=1 | D. | (a-b)2=a2-b2 |
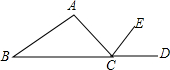 如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是60度.
如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是60度. 如图,在正方形ABCD中,如果AF=BE,那么∠AOD的度数是90°.
如图,在正方形ABCD中,如果AF=BE,那么∠AOD的度数是90°.