题目内容
2.在△ABC中,CD⊥AB于D,若AC≠BC,∠A=32°,且$\frac{A{C}^{2}}{B{C}^{2}}$=$\frac{AD}{BD}$,则∠ABC为58或122°.分析 此题分两种情况,当∠ABC是锐角,当∠ABC是钝角,由勾股定理和已知条件证得△ADC∽△BDC,得到对应角相等,结论即可求出.
解答 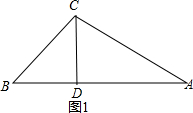 解:如图1,∵CD⊥AB,
解:如图1,∵CD⊥AB,
∴AC2=AD2+CD2,BC2=CD2+BD2,
∵$\frac{A{C}^{2}}{B{C}^{2}}$=$\frac{AD}{BD}$,
∴BD•(AD2+CD2)=AD•(CD2+BD2),
∴BD•AD(AD-BD)=CD2(AD-BD),
∴BD•AD=CD2,
∴$\frac{BD}{CD}=\frac{CD}{AD}$,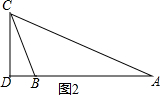
∵∠BDC=ADC,
∴△ADC∽△BDC,
∴∠B=∠ACD,
∵∠A=32°,
∴∠ABC=∠ACD=58°,
如图2,同理可知△ADC∽△BDC,
∴∠DCB=∠A=32°,
∴∠DBC=58°,
∴∠ABC=122°,
综上所述:∠ABC=58°,或122°.
点评 本题考查了相似三角形的判定和性质,勾股定理,直角三角形的性质,正确的作出图形是解题的关键.

练习册系列答案
相关题目
5.当x=1时,代数式4-3x的值是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.某市2013年底机动车的数量是2×106辆,2014年新增3×105辆,用科学记数法表示该市2014年底机动车的数量是( )
| A. | 2.3×105辆 | B. | 3.2×105辆 | C. | 2.3×106辆 | D. | 3.2×106辆 |
10.在平面直角坐标系中,点P(-3,2)关于直线y=x对称点的坐标是( )
| A. | (-3,-2) | B. | (3,2) | C. | (2,-3) | D. | (3,-2) |
7.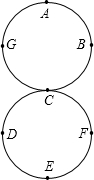 如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
 如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )| A. | D点 | B. | E点 | C. | F点 | D. | G点 |
12.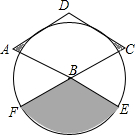 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )| A. | $\sqrt{3}$+$\frac{π}{2}$ | B. | $\sqrt{3}$+π | C. | $\sqrt{3}$-$\frac{π}{2}$ | D. | 2$\sqrt{3}$+$\frac{π}{2}$ |