题目内容
3. 如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是( )
如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,点N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连结A′C,则A′C长度的最小值是( )| A. | $\sqrt{7}$ | B. | $\sqrt{7}-1$ | C. | $\sqrt{3}$ | D. | 2 |
分析 根据题意,在N的运动过程中A′在以M为圆心、AD为直径的圆上的弧AD上运动,当A′C取最小值时,由两点之间线段最短知此时M、A′、C三点共线,得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可.
解答 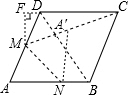 解:如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时,
解:如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时,
过点M作MF⊥DC于点F,
∵在边长为2的菱形ABCD中,∠A=60°,M为AD中点,
∴2MD=AD=CD=2,∠FDM=60°,
∴∠FMD=30°,
∴FD=$\frac{1}{2}$MD=$\frac{1}{2}$,
∴FM=DM×cos30°=$\frac{\sqrt{3}}{2}$,
∴MC=$\sqrt{F{M}^{2}+C{F}^{2}}$=$\sqrt{7}$,
∴A′C=MC-MA′=$\sqrt{7}$-1.
故选:B.
点评 此题主要考查了菱形的性质以及锐角三角函数关系等知识,得出A′点位置是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.某市2013年底机动车的数量是2×106辆,2014年新增3×105辆,用科学记数法表示该市2014年底机动车的数量是( )
| A. | 2.3×105辆 | B. | 3.2×105辆 | C. | 2.3×106辆 | D. | 3.2×106辆 |
12.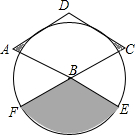 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )| A. | $\sqrt{3}$+$\frac{π}{2}$ | B. | $\sqrt{3}$+π | C. | $\sqrt{3}$-$\frac{π}{2}$ | D. | 2$\sqrt{3}$+$\frac{π}{2}$ |
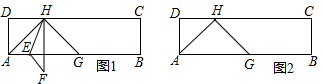
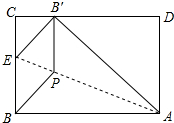 将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP.已知BC=3,CB′=1,下列结论:
将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP.已知BC=3,CB′=1,下列结论:
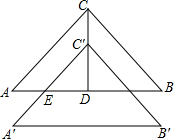 如图,Rt△ABC中,∠ACB=90°,CA=CB,AB=8,D是线段AB上的一个动点,将Rt△ABC由点C到点D的方向平移2个单位得到Rt△A′B′C′,且C′A′与AB交于点E.
如图,Rt△ABC中,∠ACB=90°,CA=CB,AB=8,D是线段AB上的一个动点,将Rt△ABC由点C到点D的方向平移2个单位得到Rt△A′B′C′,且C′A′与AB交于点E.