题目内容
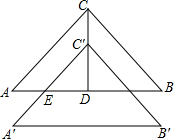
20.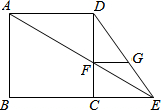 如图,点E为正方形ABCD边延长线上一点,AE交CD于F点,FG∥AD交DE于G点,其中有△ABE∽△FCE,△EFG∽△EAD,请探求CF与FG的大小关系,并说明理由.
如图,点E为正方形ABCD边延长线上一点,AE交CD于F点,FG∥AD交DE于G点,其中有△ABE∽△FCE,△EFG∽△EAD,请探求CF与FG的大小关系,并说明理由.
分析 由△CEF∽△BEA,△EFG∽△EAD,然后由相似三角形的对应边成比例,证得结论.
解答 解:CF=FG,
理由:∵四边形ABCD是正方形,
∴AB=AD,
∵△CEF∽△BEA,△EFG∽△EAD,
∴$\frac{CF}{AB}$=$\frac{EF}{AE}$,$\frac{FG}{AD}$=$\frac{EF}{AE}$,
∴$\frac{CF}{AB}$=$\frac{FG}{AD}$.
∴CF=FG.
点评 此题考查了相似三角形的判定与性质以及正方形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
5.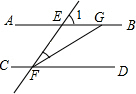 如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )
如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )
 如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )
如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )| A. | 122° | B. | 151° | C. | 116° | D. | 97° |
12.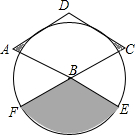 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )| A. | $\sqrt{3}$+$\frac{π}{2}$ | B. | $\sqrt{3}$+π | C. | $\sqrt{3}$-$\frac{π}{2}$ | D. | 2$\sqrt{3}$+$\frac{π}{2}$ |
10.在正方形、矩形、菱形、平行四边形、等腰梯形中,其中中心对称图形的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
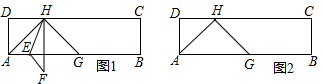
 如图,Rt△ABC中,∠ACB=90°,CA=CB,AB=8,D是线段AB上的一个动点,将Rt△ABC由点C到点D的方向平移2个单位得到Rt△A′B′C′,且C′A′与AB交于点E.
如图,Rt△ABC中,∠ACB=90°,CA=CB,AB=8,D是线段AB上的一个动点,将Rt△ABC由点C到点D的方向平移2个单位得到Rt△A′B′C′,且C′A′与AB交于点E.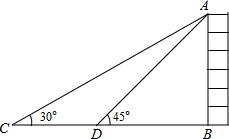 如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)