题目内容
5.某电器租赁公司有同一型号的电器设备10套.经过一段时间的经营发现:当每套电器设备的月租金为50元时,恰好全部租出.在此基础上,当每套电器设备的月租金每提高10元时,这种电器设备就少租出一套,且没租出的一套电器设备每月需支出费用(维护费、管理费等)20元.设每套电路设备的月租金为x(元),租赁公司出租该型号电器设备的月收益(收益=租金收入-支出费用)为y(元).(1)用含x的代数式表示未出租的电器设备数(套)以及所有未出租电器设备(套)的支出费用(元);
(2)求y与x之间的二次函数表达式;
(3)请把(2)中所求出的二次函数表达式配方成y=a(x+$\frac{b}{2a}$)2+$\frac{4ac-{b}^{2}}{4a}$的形式,并据此说明:当x为何值时,租赁公司出租该型号电器设备的月收益最大?最大月收益是多少?
分析 (1)根据题意可以用相应的代数式表示出未出租的电器设备数(套)和所有未出租电器设备(套)的支出费用;
(2)根据题意可以表示出y与x之间的二次函数表达式;
(3)根据(2)中函数解析式可以写出该函数的顶点式,以及求出函数的最值.
解答 解:(1)由题意可得,
未出租的电器设备数(套)是:$\frac{x-50}{10}$套,
所有未出租电器设备(套)的支出费用(元)是:$\frac{x-50}{10}×20$=(2x-100)元;
(2)由题意可得,
y=x(10-$\frac{x-50}{10}$)-(2x-100)=$-\frac{1}{10}{x}^{2}+13x+100$,
即y与x之间的二次函数表达式是y=$-\frac{1}{10}{x}^{2}+13x+100$;
(3)∵y=$-\frac{1}{10}{x}^{2}+13x+100$=$-\frac{1}{10}(x-65)^{2}+522.5$,
∵x取10的整数倍,
∴当x=60或x=70时,y取得最大值,此时y=520,
即当x为60或70时,租赁公司出租该型号电器设备的月收益最大,最大月收益是520元.
点评 本题考查二次函数的应用,解答此类题目的关键是明确题意,找出所求问题题目需要的条件,注意要联系实际情况,x取10的整数倍,为租出的机器数才是整数,这也是易错点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.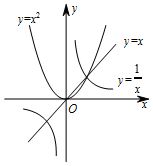 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a时,那么a<-1.
则( )
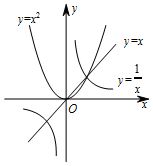 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a时,那么a<-1.
则( )
| A. | 正确的命题是①④ | B. | 错误的命题是②③④ | C. | 正确的命题是①② | D. | 错误的命题只有③ |
14.下列算式中,正确的是( )
| A. | 2x+2y=4xy | B. | 2a2+2a3=2a5 | C. | 4a2-3a2=1 | D. | -2ba2+a2b=-a2b |

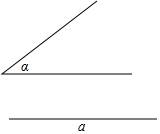 如图,已知∠α和线段a,求作△ABC,使BC=a,∠B=∠C=$\frac{1}{2}$α(只保留作图痕迹,不要求写出作法)
如图,已知∠α和线段a,求作△ABC,使BC=a,∠B=∠C=$\frac{1}{2}$α(只保留作图痕迹,不要求写出作法) 如图所示是由几个小立方体所组成几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图、左视图.
如图所示是由几个小立方体所组成几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图、左视图.