题目内容
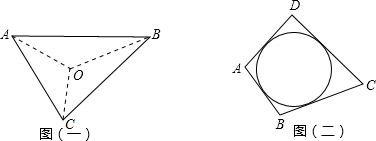
15.阅读材料:如图(一),△ABC的周长为l,内切圆O的半径为r,连接OA,OB,OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积.∵S△ABC=S△OAB+S△OBC+S△OCA
又∵S△OAB=$\frac{1}{2}$AB•r,S△OBC=$\frac{1}{2}$BC•r,S△OCA=$\frac{1}{2}$CA•r
∴S△ABC=$\frac{1}{2}$AB•r+$\frac{1}{2}$BC•r+$\frac{1}{2}$CA•r=$\frac{1}{2}$l•r
∴r=$\frac{2s}{l}$(可作为三角形内切圆半径公式)
根据上述阅读材料完成下列各题:
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,合理猜想其内切圆半径公式(不需说明理由).
分析 (1)首先证明三角形是直角三角形,再根据面积公式计算即可.
(2)连接OA、OB、OC、OD.由S四边形ABCD=S△OAB+S△OBC+S△OCD+S△AOD,由S四边形ABCD=$\frac{1}{2}$AB•r+$\frac{1}{2}$BC•r+$\frac{1}{2}$CD•r+$\frac{1}{2}$AD•r=$\frac{1}{2}$(a+b+c+d)•r=S,即可推出r=$\frac{2S}{a+b+c+d}$.
(3)类似(2)可得r=$\frac{2S}{{a}_{1}+{a}_{2}+{a}_{3}+…+{a}_{n}}$.
解答 解:(1)∵52+122=25+144=169=132,
∴边长分为5、12、13的三角形是直角三角形,
∴$\frac{1}{2}$×5×12=$\frac{1}{2}$(5+12+13)•r,
∴r=2,
∴边长分为5、12、13的三角形内切圆半径为2.
(2)如图(二)中,连接OA、OB、OC、OD.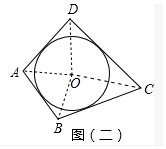
∵S四边形ABCD=S△OAB+S△OBC+S△OCD+S△AOD
又∵S△OAB=$\frac{1}{2}$AB•r,S△OBC=$\frac{1}{2}$BC•r,S△OCD=$\frac{1}{2}$CD•r,S△AOD=$\frac{1}{2}$AD•r,
∴S四边形ABCD=$\frac{1}{2}$AB•r+$\frac{1}{2}$BC•r+$\frac{1}{2}$CD•r+$\frac{1}{2}$AD•r=$\frac{1}{2}$(a+b+c+d)•r=S,
∴r=$\frac{2S}{a+b+c+d}$.
(3)若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,
其内切圆半径r=$\frac{2S}{{a}_{1}+{a}_{2}+{a}_{3}+…+{a}_{n}}$.
点评 本题考查三角形内切圆与内心、三角形的面积公式、勾股定理的逆定理等知识,解题的关键是学会用分割法求三角形的面积,属于中考常考题型.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | $\frac{1080}{x}$=$\frac{1080}{x-15}$-12 | B. | $\frac{1080}{x}$=$\frac{1080}{x-15}$+12 | ||
| C. | $\frac{1080}{x}$=$\frac{1080}{x+15}$-12 | D. | $\frac{1080}{x}$=$\frac{1080}{x+15}$+12 |
 如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB:AP=2:5,AQ=20 cm,则CQ的长是( )
如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB:AP=2:5,AQ=20 cm,则CQ的长是( )| A. | 8 cm | B. | 12 cm | C. | 30 cm | D. | 50 cm |
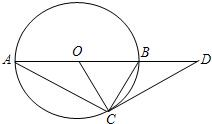 如图,AB是⊙O的直径,∠A=30°,延长OB到D,使BD=OB.
如图,AB是⊙O的直径,∠A=30°,延长OB到D,使BD=OB.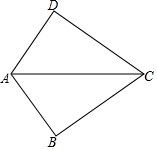 如图,△ABC≌△ADC,∠B=80°,则∠D的度数为80°.
如图,△ABC≌△ADC,∠B=80°,则∠D的度数为80°. 如图,AB与CD相交于点O,AC∥BD,AO=OB,求证:CO=OD.
如图,AB与CD相交于点O,AC∥BD,AO=OB,求证:CO=OD.