题目内容

20．如图，已知当四边形ABCD和四边形A1B1C1D1满足条件：AB=A1B1，BC=B1C1，CD=C1D1，∠B=∠B1，∠C=∠C1时，四边形ABCD与四边形A1B1C1D1全等．请你类比上述条件，写出四边形ABCD与四边形A2B2C2D2相似需要满足的条件：AB=nA1B1，BC=nB1C1，CD=nC1D1，∠B=∠B1，∠C=∠C1．

分析 根据相似多边形的判定定理和性质定理解答．

解答 解：四边形ABCD与四边形A2B2C2D2相似需要满足的条件是AB=nA1B1，BC=nB1C1，CD=nC1D1，∠B=∠B1，∠C=∠C1，
故答案为：AB=nA1B1，BC=nB1C1，CD=nC1D1，∠B=∠B1，∠C=∠C1．

点评 本题考查的是相似多边形的判定和性质，掌握相似多边形的判定定理和性质定理是解题的关键．

练习册系列答案
相关题目
10．先化简，再求值：（1-$\frac{2}{x}$）÷$\frac{{x}^{2}-4x+4}{{x}^{2}-4}$-$\frac{x+4}{x+2}$，其中x2+2x-8=0．
11．下列方程中，解为x=4的方程是（　　）
A．x-1=4B．4x=1C．4x-1=3x+3D．2（x-1）=1
8．在排成每行七天的日历表中取下一个3×3方块，若所有9个日期数之和为189，则最大的数是（　　）
A．21B．28C．29D．31
15．下表是由从1开始的连续自然数组成，观察规律并完成各题的解答．
1
2    3    4
5    6    7    8    9
10   11   12   13   14   15    16
17   18   19   20   21   22   23    24   25
26   27   28   29   30   31   32   33    34   35   36
…
（1）表中第8行的最后一个数是64，它是自然数8的平方，第8行共有15个数；
（2）用含n的代数式表示：第n行的第一个数是n2-2n+2，最后一个数是n2，第n行共有2n-1个数；
（3）求第n行各数之和（列出计算式子即可）．
5．某电器租赁公司有同一型号的电器设备10套．经过一段时间的经营发现：当每套电器设备的月租金为50元时，恰好全部租出．在此基础上，当每套电器设备的月租金每提高10元时，这种电器设备就少租出一套，且没租出的一套电器设备每月需支出费用（维护费、管理费等）20元．设每套电路设备的月租金为x（元），租赁公司出租该型号电器设备的月收益（收益=租金收入-支出费用）为y（元）．
（1）用含x的代数式表示未出租的电器设备数（套）以及所有未出租电器设备（套）的支出费用（元）；
（2）求y与x之间的二次函数表达式；
（3）请把（2）中所求出的二次函数表达式配方成y=a（x+$\frac{b}{2a}$）2+$\frac{4ac-{b}^{2}}{4a}$的形式，并据此说明：当x为何值时，租赁公司出租该型号电器设备的月收益最大？最大月收益是多少？
12．给定关于x的二次函数y=2x2+（6-2m）x+3-m，
学生甲：当m=3时，抛物线与x轴只有一个交点，因此当抛物线与x轴只有一个交点时，m的值为3；
学生乙：如果抛物线在x轴上方，那么该抛物线的最低点一定在第二象限；
请判断学生甲、乙的观点是否正确，并说明你的理由．
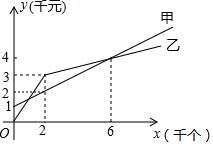9．某单位准备印制一批证书，现有两个印刷厂可供选择，甲厂费用分为制版费和印刷费两部分，乙厂直接按印刷数量收取印刷费，甲乙两厂所收取的费用y（千元）与证书数量x（千个）的函数关系图象分别如图中甲、乙所示．
（1）甲厂的制版费1千元，其证书印刷单价0.5元/张，y甲与x的函数解析式y甲=$\frac{1}{2}$x+1．
（2）请求出印刷数量x≥2时，y乙与x的函数解析式．
（3）当印制证书8千个时，应选择哪个印刷厂节省费用，节省费用多少元？
（4）如果甲厂想把8千个证书的印制工作承揽下来，在不降低制版费的前提下，每个证书最少降低多少元？
10．如图，已知正方形ABCD，顶点A（1，3）、B（1，1）、C（3，1），规定“把正方形ABCD先沿x轴翻折，再向左平移1个单位”为一次交换，如此这样，连续经过2016次变换后，正方形ABCD的对角线交点M的坐标变为（-2014，2）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网