题目内容
13.为了节约用水,某市规定:每户居民每月用水不超过20立方米,按每立方米2元收费;超过20立方米,则超过的部分按每立方米4元收费.如果某户居民十月份缴纳水费52元,则该户居民十月份实际用水为23立方米.分析 由20×2=40,40<42即可得出则该户居民十月份实际用水超过20立方米.设该户居民十月份实际用水为x立方米,根据缴纳水费钱数=20×2+(时间用水量-20)×4即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:∵20×2=40(元),40<52,
∴则该户居民十月份实际用水超过20立方米.
设该户居民十月份实际用水为x立方米,
根据题意得:20×2+4(x-20)=52,
解得:x=23.
故答案为:23.
点评 本题考查了一元一次方程的应用,根据数量关系纳水费钱数=20×2+(时间用水量-20)×4列出关于x的一元一次方程是解题的关键.

练习册系列答案
相关题目
3.某单位向一所希望小学赠送1080件文具,现用A,B两种不同的包装箱进行包装,已知每个B型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个,设B型包装箱每个可以装x件文具,根究题意列方程为( )
| A. | $\frac{1080}{x}$=$\frac{1080}{x-15}$-12 | B. | $\frac{1080}{x}$=$\frac{1080}{x-15}$+12 | ||
| C. | $\frac{1080}{x}$=$\frac{1080}{x+15}$-12 | D. | $\frac{1080}{x}$=$\frac{1080}{x+15}$+12 |
4. 如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB:AP=2:5,AQ=20 cm,则CQ的长是( )
如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB:AP=2:5,AQ=20 cm,则CQ的长是( )
 如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB:AP=2:5,AQ=20 cm,则CQ的长是( )
如图是小刘做的一个风筝支架示意图,已知BC∥PQ,AB:AP=2:5,AQ=20 cm,则CQ的长是( )| A. | 8 cm | B. | 12 cm | C. | 30 cm | D. | 50 cm |
8.在排成每行七天的日历表中取下一个3×3方块,若所有9个日期数之和为189,则最大的数是( )
| A. | 21 | B. | 28 | C. | 29 | D. | 31 |
2.已知8a3bm÷(28anb2)=$\frac{2}{7}$b3,则m-n的值为( )
| A. | 3 | B. | 6 | C. | 2 | D. | -33 |
3.若a<-1,则方程x2+(1-2a)x+a2=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实根 | ||
| C. | 没有实数根 | D. | 不能确定 |
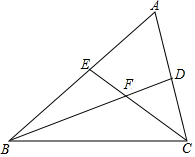 如图,△ABC的∠B和∠C的平分线BD,CE相交于点F,∠A=60°,
如图,△ABC的∠B和∠C的平分线BD,CE相交于点F,∠A=60°,