题目内容
2.四边形ABCD对角线互相垂直,顺次连接四边形ABCD四边中点得到的四边形是矩形.分析 根据四边形对角线互相垂直,运用三角形中位线平行于第三边证明四个角都是直角,判断是矩形.
解答 解:
如图,∵E、F、G、H分别为各边中点,
∴EF∥GH∥DB,EF=GH=$\frac{1}{2}$DB,EH=FG=$\frac{1}{2}$AC,EH∥FG∥AC,
∵DB⊥AC,
∴EF⊥EH,
∴四边形EFGH是矩形.
故答案为:矩形.
点评 本题考查中点四边形,解题时主要是利用了三角形中位线定理的性质,比较简单,也可以利用三角形的相似,得出正确结论.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
10.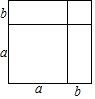 如图,能根据图形中的面积说明的乘法公式是( )
如图,能根据图形中的面积说明的乘法公式是( )
 如图,能根据图形中的面积说明的乘法公式是( )
如图,能根据图形中的面积说明的乘法公式是( )| A. | (a+b)(a-b)=a2-b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | (a-b)=a2-2ab+b2 | D. | (x+p)(x+q)=x2+(p+q)x+pq |
11. 如图,在等腰△ABC顶角A=36°,两底角的平分线BD、CE交于点F,则图中等腰三角形的个数为( )
如图,在等腰△ABC顶角A=36°,两底角的平分线BD、CE交于点F,则图中等腰三角形的个数为( )
 如图,在等腰△ABC顶角A=36°,两底角的平分线BD、CE交于点F,则图中等腰三角形的个数为( )
如图,在等腰△ABC顶角A=36°,两底角的平分线BD、CE交于点F,则图中等腰三角形的个数为( )| A. | 6个 | B. | 8个 | C. | 10个 | D. | 12个 |
12.原命题为:“若a>0,b>0,则a+b>0”,逆命题为:“若a+b>0,则a>0,b>0”.下列判定正确的是( )
| A. | 原命题为真命题,逆命题为假命题 | B. | 原命题与逆命题均为真命题 | ||
| C. | 原命题为假命题,逆命题为真命题 | D. | 原命题与逆命题均为假命题 |
 将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为15°.
将一副三角板如图放置,使点A在DE上,BC∥DE,则∠ACE的度数为15°. 如图,AB∥CD,∠EAC=∠EAB,∠ECA=∠ECD,则∠AEC=90度.
如图,AB∥CD,∠EAC=∠EAB,∠ECA=∠ECD,则∠AEC=90度. 如图,在Rt△ABC中,∠A=90°,AB=6,BC=10,D是AC上一点,CD=5,DE⊥BC于E.求线段DE的长.
如图,在Rt△ABC中,∠A=90°,AB=6,BC=10,D是AC上一点,CD=5,DE⊥BC于E.求线段DE的长.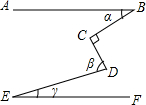 如图,AB∥EF,∠C=90°,写出α、β、γ之间的等量关系是α+β-γ=90°.
如图,AB∥EF,∠C=90°,写出α、β、γ之间的等量关系是α+β-γ=90°. 在△ABC中,作MN∥BC,且MN分别交AB,AC于点M,N两点;若AM=1,BM=3,MN=$\frac{3}{2}$,则BC的长为6.
在△ABC中,作MN∥BC,且MN分别交AB,AC于点M,N两点;若AM=1,BM=3,MN=$\frac{3}{2}$,则BC的长为6.