题目内容
14. 在△ABC中,作MN∥BC,且MN分别交AB,AC于点M,N两点;若AM=1,BM=3,MN=$\frac{3}{2}$,则BC的长为6.
在△ABC中,作MN∥BC,且MN分别交AB,AC于点M,N两点;若AM=1,BM=3,MN=$\frac{3}{2}$,则BC的长为6.
分析 由MN∥BC可得出∠AMN=∠ABC、∠ANM=∠ACB,进而可得出△AMN∽△ABC,根据相似三角形的性质可得出$\frac{AM}{AB}$=$\frac{MN}{BC}$,代入各边长可求出BC的长.
解答 解:∵MN∥BC,
∴∠AMN=∠ABC,∠ANM=∠ACB,
∴△AMN∽△ABC,
∴$\frac{AM}{AB}$=$\frac{MN}{BC}$,即$\frac{1}{1+3}$=$\frac{\frac{3}{2}}{BC}$,
∴BC=6.
故答案为:6.
点评 本题考查了相似三角形的判定与性质,根据△AMN∽△ABC找出$\frac{AM}{AB}$=$\frac{MN}{BC}$是解题的关键.

练习册系列答案
相关题目
4.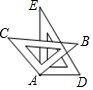 如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )
如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )
 如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )
如图,将一副三角板的直角顶点重合放置于A处(两块三角板可以在同一平面内自由转动),则下列结论一定成立的是( )| A. | ∠BAD≠∠EAC | B. | ∠DAC-∠BAE=45° | C. | ∠DAC+∠BAE=180° | D. | ∠DAC-∠BAE=90° |
5.储蓄所先后办理了7笔业务,取出9.5万元,存入5万元,取出8万元,存入12万元,存入25万元,取出10.25万元,取出2万元,这时的存款比最初( )
| A. | 增加12.25万元 | B. | 减少12.25万元 | C. | 增加12万元 | D. | 减少12万元 |
4.已知|a|=3,那么a=( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 不存在 |
 如图,在一块长为30米,宽为16米的长方形草地上,有两条宽都为1米的纵、横相交的小路,这块草地的绿地面积为435平方米.
如图,在一块长为30米,宽为16米的长方形草地上,有两条宽都为1米的纵、横相交的小路,这块草地的绿地面积为435平方米.
 如图,三角板的直角顶点在直线AB上,已知∠1=50°,则∠2的度数是40°.
如图,三角板的直角顶点在直线AB上,已知∠1=50°,则∠2的度数是40°.