Question

12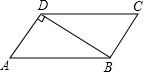．如图，在?ABCD中，连接BD，AD⊥BD，AB=4cm，BD=3cm，则?ABCD的面积为3$\sqrt{7}$cm²．

Answer 1

分析 先根据勾股定理求得AD的长，再根据平行四边形的面积公式进行计算即可．

解答 解：∵?ABCD中，AD⊥BD，AB=4cm，BD=3cm，
∴Rt△ABD中，AD=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$，
∴?ABCD的面积=AD×BD=3$\sqrt{7}$．
故答案为：3$\sqrt{7}$．

点评 本题主要考查了平行四边形的性质，解决问题的关键是掌握勾股定理的运用．在直角三角形中，已知两边的长，可以求得第三边的长．