题目内容
7.若不等式组$\left\{\begin{array}{l}{x-a>2}\\{b-2x>0}\end{array}\right.$的解集是-1<x<1,则(a+b)2014等于1.分析 先去用a、b表示出不等式组的解集,然后根据不等式组的解集列出关于a、b的方程组并求出a、b,最后代入代数式进行计算即可得解.
解答 解:$\left\{\begin{array}{l}{x-a>2①}\\{b-2x>0②}\end{array}\right.$,
解不等式①得,x>2+a,
解不等式②得,x<$\frac{b}{2}$,
所以,不等式组的解集是2+a<x<$\frac{b}{2}$,
∵不等式组的解集是-1<x<1,
∴$\left\{\begin{array}{l}{2+a=-1}\\{\frac{b}{2}=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-3}\\{b=2}\end{array}\right.$,
所以,(a+b)2014=(-3+2)2014=1.
故答案为:1.
点评 本题主要考查了一元一次不等式组解集的求法,难点在于用a、b表示出不等式组的解集再列出方程组.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c). 如图,在△ABC中,AB=10,BC=12,以AB为直径的⊙O交BC于点D.过点D的⊙O的切线垂直AC于点F,交AB的延长线于点E.
如图,在△ABC中,AB=10,BC=12,以AB为直径的⊙O交BC于点D.过点D的⊙O的切线垂直AC于点F,交AB的延长线于点E.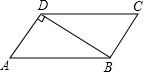 如图,在?ABCD中,连接BD,AD⊥BD,AB=4cm,BD=3cm,则?ABCD的面积为3$\sqrt{7}$cm2.
如图,在?ABCD中,连接BD,AD⊥BD,AB=4cm,BD=3cm,则?ABCD的面积为3$\sqrt{7}$cm2. 如图,以△ABC的边AB为直径的⊙O交AC边于点D,且过点D的⊙O的切线DE平分BC边,交BC于点E.
如图,以△ABC的边AB为直径的⊙O交AC边于点D,且过点D的⊙O的切线DE平分BC边,交BC于点E. 已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点A(1,2).
已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点A(1,2).