题目内容
4.若关于x的方程kx2+x+1=0有实根,求k的取值范围.分析 分类讨论:当k=0,原方程变形为x+1=0,解得x=-1;当k≠0,则△=1-4×k≥0,原方程有两个实数根,得到k≤$\frac{1}{4}$且k≠0时,原方程有两个实数根,然后综合两种情况得到k的取值范围.
解答 解:当k=0,原方程变形为x+1=0,解得x=-1;
当k≠0,则△=1-4×k≥0,原方程有两个实数根,解得k≤$\frac{1}{4}$,
即k≤$\frac{1}{4}$且k≠0时,原方程有两个实数根.
所以k的取值范围是k≤$\frac{1}{4}$.
点评 本题主要考查了根的判别式的知识,方程有实数根则△≥0,此题还需要注意分类讨论思想.

练习册系列答案
相关题目
14.若$\left\{\begin{array}{l}{x+y=16}\\{\sqrt{y+5}-\sqrt{x-1}=2}\end{array}\right.$,则(y-2)1-x的值为( )
| A. | 729 | B. | $\frac{1}{729}$ | C. | 6561 | D. | $\frac{1}{6561}$ |
13.化分式方程$\frac{1}{5{x}^{2}-5}$-$\frac{3}{{x}^{2}-1}$-$\frac{4}{1-x}$=0为整式方程时,方程两边同乘( )
| A. | (5x2-5)(x2-1)(1-x) | B. | 5(x2-1)(1-x) | C. | 5(x2-1)(x+1) | D. | 5(x+1)(x-1) |
14.下列图形中,是中心对称图形,但不是轴对称图形的是( )
| A. | 矩形 | B. | 平行四边形 | C. | 直角梯形 | D. | 等腰梯形 |
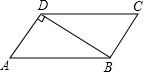 如图,在?ABCD中,连接BD,AD⊥BD,AB=4cm,BD=3cm,则?ABCD的面积为3$\sqrt{7}$cm2.
如图,在?ABCD中,连接BD,AD⊥BD,AB=4cm,BD=3cm,则?ABCD的面积为3$\sqrt{7}$cm2. 如图,以△ABC的边AB为直径的⊙O交AC边于点D,且过点D的⊙O的切线DE平分BC边,交BC于点E.
如图,以△ABC的边AB为直径的⊙O交AC边于点D,且过点D的⊙O的切线DE平分BC边,交BC于点E.