题目内容
2. 如图,直线l1∥l2,∠α=∠β,∠1=50°,则∠2=130°.
如图,直线l1∥l2,∠α=∠β,∠1=50°,则∠2=130°.
分析 先根据平行线的性质,由l1∥l2得∠3=∠1=40°,再根据平行线的判定,由∠α=∠β得AB∥CD,然后根据平行线的性质得∠2+∠3=180°,再把∠1=40°代入计算即可.
解答 解:如图,
∵ l1∥l2,
l1∥l2,
∴∠3=∠1=50°,
∵∠α=∠β,
∴AB∥CD,
∴∠2+∠3=180°,
∴∠2=180°-∠3=180°-50°=130°.
故答案为:130°.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
相关题目
13.化分式方程$\frac{1}{5{x}^{2}-5}$-$\frac{3}{{x}^{2}-1}$-$\frac{4}{1-x}$=0为整式方程时,方程两边同乘( )
| A. | (5x2-5)(x2-1)(1-x) | B. | 5(x2-1)(1-x) | C. | 5(x2-1)(x+1) | D. | 5(x+1)(x-1) |
14.下列图形中,是中心对称图形,但不是轴对称图形的是( )
| A. | 矩形 | B. | 平行四边形 | C. | 直角梯形 | D. | 等腰梯形 |
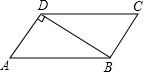 如图,在?ABCD中,连接BD,AD⊥BD,AB=4cm,BD=3cm,则?ABCD的面积为3$\sqrt{7}$cm2.
如图,在?ABCD中,连接BD,AD⊥BD,AB=4cm,BD=3cm,则?ABCD的面积为3$\sqrt{7}$cm2. 已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点A(1,2).
已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点A(1,2).