题目内容
2.已知xyz≠0,且$\left\{\begin{array}{l}{x+2y+z=0}\\{5x+4y-4z=0}\end{array}\right.$,求$\frac{{x}^{2}+6{y}^{2}-10{z}^{2}}{3{x}^{2}-4yz+5{z}^{2}}$的值.分析 把z看成已知数,求出x、y,然后代入化简即可.
解答 解:由$\left\{\begin{array}{l}{x+2y+z=0}\\{5x+4y-4z=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=2z}\\{y=-\frac{3}{2}z}\end{array}\right.$,
∴原式=$\frac{4{z}^{2}+6×\frac{9}{4}{z}^{2}-10{z}^{2}}{3×4{z}^{2}+6{z}^{2}+5{z}^{2}}$=$\frac{15}{46}$.
点评 本题考查分式的值,解三元方程组等知识,解题的关键是把z看成已知数解方程组,属于中考常考题型.

练习册系列答案
相关题目
12.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.若$\left\{\begin{array}{l}{x+y=16}\\{\sqrt{y+5}-\sqrt{x-1}=2}\end{array}\right.$,则(y-2)1-x的值为( )
| A. | 729 | B. | $\frac{1}{729}$ | C. | 6561 | D. | $\frac{1}{6561}$ |
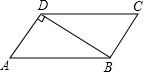 如图,在?ABCD中,连接BD,AD⊥BD,AB=4cm,BD=3cm,则?ABCD的面积为3$\sqrt{7}$cm2.
如图,在?ABCD中,连接BD,AD⊥BD,AB=4cm,BD=3cm,则?ABCD的面积为3$\sqrt{7}$cm2.