题目内容
如图，在△ABC中，已知∠B=70°，将△ABC绕点A逆时针旋转，使点B落在BC边上的D处，则∠CAE=考点：旋转的性质
专题：
分析：根据旋转可得AB=AD，∠BAD=∠CAE，然后根据等边对等角可得∠B=∠ADB=70°，再利用三角形内角和定理可以计算出∠BAD的度数，进而得到∠CAE的度数．
解答：解：根据旋转可得AB=AD，∠BAD=∠CAE，
∵AB=AD，∠B=70°，
∴∠B=∠ADB=70°，
∴∠BAD=180°-70°-70°=40°，
∴∠CAE=40°，
故答案为：40°．
∵AB=AD，∠B=70°，
∴∠B=∠ADB=70°，
∴∠BAD=180°-70°-70°=40°，
∴∠CAE=40°，
故答案为：40°．
点评：此题主要考查了旋转的性质，关键是找出旋转后相等的线段和相等的角．
练习册系列答案
轻松暑假总复习系列答案
相关题目
若a=(
)-2，b=(-1)-1，c=(-
)0，则a、b、c的大小关系是（ ）
| 1 |
| 2 |
| π |
| 2 |
| A、a＞b＞c |
| B、a＞c＞b |
| C、c＞a＞b |
| D、c＞b＞a |
如图，每个小正方形的边长都是1．
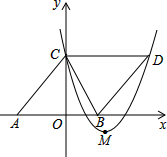如图，在平面直角坐标系xOy中，菱形ABDC的边AB在x轴上，顶点C在y轴上，A（-6，0），C（0，8），抛物线y=ax2-10ax+c经过点C，且顶点M在直线BC上，则抛物线解析式为
如图，AB是半圆直径，半径OC⊥AB于点O，点D是弧BC的中点，连结CD、AD、OD，给出以下四个结论：
如图，在平面直角坐标系中，直线AB交x轴于点A（a，0），交y轴于点B（0，b），且a、b满足