题目内容
 如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足
如图,在平面直角坐标系中,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足| a-4 |
(1)求S△AOB;
(2)过点M作MC⊥AB交y轴于点C,求点C的坐标.
考点:一次函数的性质
专题:
分析:(1)先根据非负数的性质求出a、b的值,再根据三角形的面积公式即可求解;
(2)先求出M点的坐标,再根据互相垂直的两条直线斜率之积为-1,求出直线CM的斜率,然后将M点坐标代入,得到直线CM的解析式,进而得到点C的坐标.
(2)先求出M点的坐标,再根据互相垂直的两条直线斜率之积为-1,求出直线CM的斜率,然后将M点坐标代入,得到直线CM的解析式,进而得到点C的坐标.
解答:解:(1)∵
+(b-2)2=0,
∴a-4=0,b-2=0,
∴a=4,b=2,
∴S△AOB=
×4×2=4;
(2)∵直线AB交x轴于点A(4,0),交y轴于点B(0,2),
∴直线AB的解析式为y=-
x+2,
当x=y时,x=y=
,
∴M(
,
).
设直线CM的解析式为y=2x+b,则
=2×
+b,b=-
,
即y=2x-
,
当x=0时,y=-
,
∴点C的坐标为(0,-
).
| a-4 |
∴a-4=0,b-2=0,
∴a=4,b=2,
∴S△AOB=
| 1 |
| 2 |
(2)∵直线AB交x轴于点A(4,0),交y轴于点B(0,2),
∴直线AB的解析式为y=-
| 1 |
| 2 |
当x=y时,x=y=
| 4 |
| 3 |
∴M(
| 4 |
| 3 |
| 4 |
| 3 |
设直线CM的解析式为y=2x+b,则
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
即y=2x-
| 4 |
| 3 |
当x=0时,y=-
| 4 |
| 3 |
∴点C的坐标为(0,-
| 4 |
| 3 |
点评:本题考查了非负数的性质,一次函数的性质,三角形的面积,难度适中.掌握互相垂直的两条直线斜率之积为-1,是解(2)题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
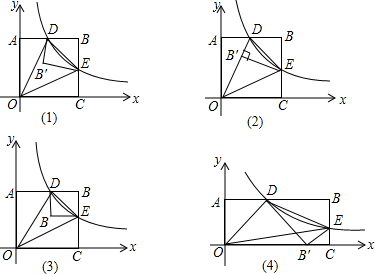
 如图,在△ABC中,已知∠B=70°,将△ABC绕点A逆时针旋转,使点B落在BC边上的D处,则∠CAE=
如图,在△ABC中,已知∠B=70°,将△ABC绕点A逆时针旋转,使点B落在BC边上的D处,则∠CAE=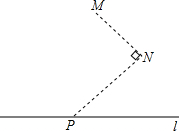 如图所示,在水渠l的同一侧有两个水池M与N,把水渠水先引到水池N,再由N引人水池M.连接MN,作∠MNP=90°,NP交l于点P,将水渠水由P放到N,再由N放到M,所行路径最短,对吗?如果不对,你是怎样设计的?写出你的设计方案.
如图所示,在水渠l的同一侧有两个水池M与N,把水渠水先引到水池N,再由N引人水池M.连接MN,作∠MNP=90°,NP交l于点P,将水渠水由P放到N,再由N放到M,所行路径最短,对吗?如果不对,你是怎样设计的?写出你的设计方案.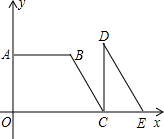 四边形OABC是直角梯形,△CDE是直角三角形,点A在y轴上,点C、E在x轴上,BC∥DE,抛物线y=-
四边形OABC是直角梯形,△CDE是直角三角形,点A在y轴上,点C、E在x轴上,BC∥DE,抛物线y=- 如图,已知一次函数y1=x-6与反比例函数y2=
如图,已知一次函数y1=x-6与反比例函数y2=