题目内容
5.(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;(2)阅读下面的内容,并解决后面的问题:
如图2,AP、CP分别平分∠BAD.∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数;
解:∵AP、CP分别平分∠BAD.∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得:$\left\{\begin{array}{l}{∠P+∠3=∠1+∠B①}\\{∠P+∠2=∠4+∠D②}\end{array}\right.$
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P=$\frac{1}{2}$(∠B+∠D)=26°.
①如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
②在图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
③在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
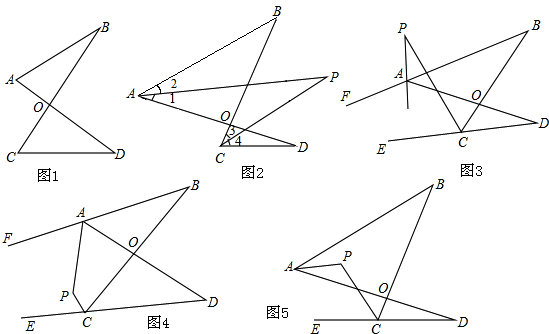
分析 (1)根据三角形的内角和等于180°列式整理即可得证;
(2)根据角平分线的定义可得∠1=∠2,∠3=∠4,再根据(1)的结论列出整理即可得解;
①表示出∠PAD和∠PCD,再根据(1)的结论列出等式并整理即可得解;
②根据四边形的内角和等于360°可得(180°-∠1)+∠P+∠4+∠B=360°,∠2+∠P+(180°-∠3)+∠D=360°,然后整理即可得解;
③根据(1)的结论∠B+∠BAD=∠D+∠BCD,∠PAD+∠P=∠D+∠PCD,然后整理即可得解.
解答 解:(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180゜,
∴∠A+∠B+∠AOB=∠C+∠D+∠COD.
∵∠AOB=∠COD,
∴∠A+∠B=∠C+∠D;
(2)①如图3,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴∠PAD=180°-∠2,∠PCD=180°-∠3,
∵∠P+(180°-∠1)=∠D+(180°-∠3),
∠P+∠1=∠B+∠4,
∴2∠P=∠B+∠D,
∴∠P=$\frac{1}{2}$(∠B+∠D)=$\frac{1}{2}$×(36°+16°)=26°;
②如图4,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∴(180°-2∠1)+∠B=(180°-2∠4)+∠D,
在四边形APCB中,(180°-∠1)+∠P+∠4+∠B=360°,
在四边形APCD中,∠2+∠P+(180°-∠3)+∠D=360°,
∴2∠P+∠B+∠D=360°,
∴∠P=180°-$\frac{1}{2}$(∠B+∠D);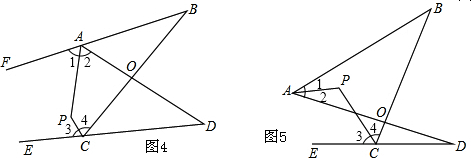
③如图5,∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,
∴∠1=∠2,∠3=∠4,
∵(∠1+∠2)+∠B=(180°-2∠3)+∠D,
∠2+∠P=(180°-∠3)+∠D,
∴2∠P=180°+∠D+∠B,
∴∠P=90°+$\frac{1}{2}$(∠B+∠D).
点评 本题考查了三角形的内角和定理,角平分线的定义,准确识图并运用好“8字形”的结论,然后列出两个等式是解题的关键,用阿拉伯数字加弧线表示角更形象直观.

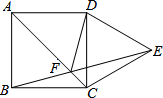 如图,以正方形ABCD的CD边长作等边△DCE,AC和BE交于点F,连接DF.
如图,以正方形ABCD的CD边长作等边△DCE,AC和BE交于点F,连接DF.
 如图,△ABC中,AB=BC=5,AC=6,过点A作AD∥BC,点P、Q分别是射线AD、线段BA上的动点(不与A、B重合),且AP=BQ,过点P作PE∥AC交线段AQ于点O,连接PQ,设△POQ面积为y,AP=x.
如图,△ABC中,AB=BC=5,AC=6,过点A作AD∥BC,点P、Q分别是射线AD、线段BA上的动点(不与A、B重合),且AP=BQ,过点P作PE∥AC交线段AQ于点O,连接PQ,设△POQ面积为y,AP=x.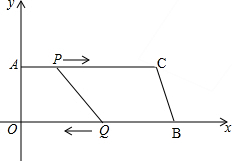 如图,在四边形AOBC中,AC∥OB,顶点O是原点,顶点A的坐标为(0,8),AC=24cm,OB=26cm,点P从点A出发,以1cm/s的速度向点C运动,点Q从点B同时出发,以3m/s的速度向点O运动.规定其中一个动点到达端点时,另一个动点也随之停止运动;从运动开始,设P(Q)点运动的时间为ts.
如图,在四边形AOBC中,AC∥OB,顶点O是原点,顶点A的坐标为(0,8),AC=24cm,OB=26cm,点P从点A出发,以1cm/s的速度向点C运动,点Q从点B同时出发,以3m/s的速度向点O运动.规定其中一个动点到达端点时,另一个动点也随之停止运动;从运动开始,设P(Q)点运动的时间为ts.