题目内容
15.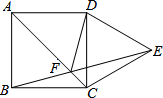 如图,以正方形ABCD的CD边长作等边△DCE,AC和BE交于点F,连接DF.
如图,以正方形ABCD的CD边长作等边△DCE,AC和BE交于点F,连接DF.(1)求∠CBE的度数;
(2)求证:AF=EF.
分析 (1)由正方形和等边三角形的性质得出BC=CE,∠BCE=150°,由等腰三角形的性质和三角形内角和定理即可得出结果;
(2)由SAS证明△BCF≌△CDF,得出∠CBF=∠CDF=15°,求出∠ADF=∠EDF,由SAS证明△ADF≌△EDF,即可得出结论.
解答 (1)解:∵四边形ABCD是正方形,
∴BC=DC,∠ABC=∠BCD=∠ADC=90°,∠BCF=∠DCF=45°,
∵△DCE是等边三角形,
∴DC=CE=DE,∠CDE=∠DCE=∠DEC=60°,
∴BC=CE,∠BCE=90°+60°=150°,
∴∠CBE=∠CEB=$\frac{1}{2}$(180°-150°)=15°;
(2)证明:在△BCF和△CDF中,
$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCF=∠DCF}&{\;}\\{CF=CF}&{\;}\end{array}\right.$,
∴△BCF≌△CDF(SAS),
∴∠CBF=∠CDF=15°,
∴∠ADF=90°-15°=75°,∠EDF=60°+15°=75°,
∴∠ADF=∠EDF,
在△ADF和△EDF中,
$\left\{\begin{array}{l}{AD=DE}&{\;}\\{∠ADF=∠EDF}&{\;}\\{DF=DF}&{\;}\end{array}\right.$,
∴△ADF≌△EDF(SAS),
∴AF=EF.
点评 本题考查了正方形的性质、等边三角形的性质、全等三角形的判定与性质、等腰三角形的判定与性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
6.4的平方根是( )
| A. | ±16 | B. | 2 | C. | ±2 | D. | ±$\sqrt{2}$ |
3. 如图,?ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE等于( )
如图,?ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE等于( )
 如图,?ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE等于( )
如图,?ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE等于( )| A. | 65° | B. | 25° | C. | 30° | D. | 15° |
10.解分式方程$\frac{x}{3+x}$-$\frac{2}{2+x}$=1时,去分母后可得到( )
| A. | x(2+x)-2( 3+x)=1 | B. | x(2+x)-2=2+x | ||
| C. | x(2+x)-2( 3+x)=(2+x)(3+x) | D. | x-2( 3+x)=3+x |
7.点A(a,4)与点B(3,b)关于x轴对称,则(a+b)2013的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 72013 |
 如图1,在△ABC中,CA=CB=4,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么BE的值为$\frac{7\sqrt{2}}{3}$.
如图1,在△ABC中,CA=CB=4,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么BE的值为$\frac{7\sqrt{2}}{3}$.